Applied Fluid Mechanics Lab Manual Copyright © 2019 by Habib Ahmari and Shah Md Imran Kabir is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.
Mavs Open Press
Arlington
Applied Fluid Mechanics Lab Manual Copyright © 2019 by Habib Ahmari and Shah Md Imran Kabir is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.
1
If you are an instructor who is using this OER for a course, please let us know by filling out our OER Adoption Form.
Creation of this resource was supported by Mavs Open Press, operated by the University of Texas at Arlington Libraries (UTA Libraries). Mavs Open Press offers no-cost services for UTA faculty, staff, and students who wish to openly publish their scholarship. The Libraries’ program provides human and technological resources that empower our communities to publish new open access journals, to convert traditional print journals to open access publications, and to create or adapt open educational resources (OER). Our resources are openly licensed using Creative Commons licenses and are offered in various e-book formats free of charge, which can be downloaded from the Mavs Open Press OER catalog. Optional print copies of this text may be available through the UTA Bookstore or can be purchased directly from XanEdu, Mavs Open Press’ exclusive print provider and distributor.
OER are free teaching and learning materials that are licensed to allow for revision and reuse. They can be fully self-contained textbooks, videos, quizzes, learning modules, and more. OER are distinct from public resources in that they permit others to use, copy, distribute, modify, or reuse the content. The legal permission to modify and customize OER to meet the specific learning objectives of a particular course make them a useful pedagogical tool.
Pressbooks is an open source, web-based authoring tool based on WordPress, and it is the primary tool that Mavs Open Press uses to create and adapt course materials. Pressbooks should not be used with Internet Explorer. The following browsers are best to use with Pressbooks:
Information about open education at UTA is available online. Contact us at oer@uta.edu for other inquires related to UTA Libraries publishing services.
2
Creation of this OER was funded by the UTA CARES Grant Program, which is sponsored by UTA Libraries. Under the auspices of UTA’s Coalition for Alternative Resources in Education for Students (CARES), the grant program supports educators interested in practicing open education through the adoption of OER and, when no suitable open resource is available, through the creation of new OER or the adoption of library-licensed or other free content. Additionally, the program promotes innovation in teaching and learning through the exploration of open educational practices, such as collaborating with students to produce educational content of value to a wider community. Information about the grant program and funded projects is available online.
This OER is designed for a junior-level lab in applied fluid mechanics (CE 3142) at UTA. The lack of standard material for the fluid mechanics laboratory course causes students to seek help from several textbooks in the subject area for the theoretical background of experiments, which costs them money and time; others seek out online resources for lab demonstrations. Even though free resources (e.g. lab manuals, videos, lab reports) are increasingly available on the Internet, they are too frequently inadequate and unreliable. This manual supports students by providing streamlined, vetted, and self-paced content, which frees students’ time and saves them money. The OER includes customized lab manuals, educational videos, and an interactive lab report preparation workbooks for ten fluid mechanics experiments. Each section includes theory, practical applications, objectives, experimental procedure, and post-experiment questions. Preparation of result tables and charts are automated within the workbook for each experiment to facilitate answering post-experiment questions and writing lab reports.
In Summer 2017, Dr. Habib Ahmari taught the Fluid Mechanics Lab at UTA for the first time. He found students struggling with lab manuals that were prepared by previous instructors. Despite the fact that laboratory courses are considered essential components of engineering programs, there are no standard textbooks available for such courses. The lab teaching materials are usually developed by lab instructors (as handouts) or lab equipment manufactures as instruction manuals. These types of course materials are narratives and do not match very well with the nature of these courses; thus students rarely make connections with them. After teaching the course for two semesters, Dr. Ahmari realized it was very difficult for students to visualize the experimental procedures by reading these narratives. He also noticed that some students would videotape him or teaching assistants demonstrating the experimental procedure for future references. These observations triggered the idea of developing an OER for the course.
Dr. Ahmari was awarded a UTA CARES Innovation Grant in 2018 to develop an OER to support transitioning the traditional Fluid Mechanics Lab to a media-rich, student-paced learning environment. Shah Md Imran Kabir (graduate student) and Andrew Czubai, Ankur Patel, Nicholas Sopko (undergraduate students) were recruited for this project. This dedicated team worked on this project during the summer to make sure the platform would be ready for implementation for Fall 2018. Creation of the OER project included five steps. The first step was to shoot eleven educational videos of the lab experiments. For this work, two groups of two students were formed. The first group assisted with preparing scripts for videos, demonstrating experiments in the Fluid Mechanics Laboratory of the Civil Engineering Department, and providing voice over of the video. The second group performed video recording, editing, and adding closed captioning. In the next step, lab manuals for ten lab experiments were developed by Dr. Ahmari and his graduate student, Shah Md Imran Kabir. The lab manual was reviewed by a professional editor to enhance the quality of the material. Next, the team prepared the necessary workbooks for each of the experiments that can be used by students to record their raw data as input. The result tables and graphs will be automatically prepared within the workbook as output. All components of this OER (i.e. lab manuals, videos, and report preparing workbooks) were shared with students enrolled in Fluid Mechanics Lab in Fall 2018 via Blackboard. In Summer 2019, the manual was published in Pressbooks with videos and workbooks embedded in the text.
Habib Ahmari, Ph. D., P.E. is an Assistant Professor of Instruction and the Director of the Learning Center in the Department of Civil Engineering at UTA. He has more than 15 years of industry, education, and research experience. He has developed and taught several graduate and undergraduate courses in the area of water resources engineering.
Shah Md Imran Kabir is a graduate student in the Department of Civil Engineering at UTA. He completed his B.Sc. in water resources engineering from Bangladesh University of Engineering and Technology. He has 2 years of working experience in the water resources engineering industry.
3
Habib Ahmari, Ph.D., P.E. – Assistant Professor of Instruction, University of Texas at Arlington
Shah Md Imran Kabir – Graduate Teaching Assistant, University of Texas at Arlington
Andrew Czubai – University of Texas at Arlington undergraduate student, Civil Engineering
Ankur Patel – University of Texas at Arlington undergraduate student, Civil Engineering
Nicholas Sopko – University of Texas at Arlington undergraduate student, Civil Engineering
Ginny Bowers – former administrative assistant for UTA Department of Civil Engineering (retired)
Michelle Reed, Brittany Griffiths, Kartik Mann, and Thomas Perappadan of UTA Libraries for assisting in the publication of this resource.
Brittany Griffiths, UTA Libraries’ Publishing Specialist, designed the cover for this OER. The image used is Cascade and Ponds, Cooper Street, Arlington, Texas, and was taken by the author, Habib Ahmari.
I
Basic knowledge about fluid mechanics is required in various areas of water resources engineering such as designing hydraulic structures and turbomachinery. The applied fluid mechanics laboratory course is designed to enhance civil engineering students’ understanding and knowledge of experimental methods and the basic principle of fluid mechanics and apply those concepts in practice. The lab manual provides students with an overview of ten different fluid mechanics laboratory experiments and their practical applications. The objective, practical applications, methods, theory, and the equipment required to perform each experiment are presented. The experimental procedure, data collection, and presenting the results are explained in detail.
1
Hydrostatic forces are the resultant force caused by the pressure loading of a liquid acting on submerged surfaces. Calculation of the hydrostatic force and the location of the center of pressure are fundamental subjects in fluid mechanics. The center of pressure is a point on the immersed surface at which the resultant hydrostatic pressure force acts.
The location and magnitude of water pressure force acting on water-control structures, such as dams, levees, and gates, are very important to their structural design. Hydrostatic force and its line of action is also required for the design of many parts of hydraulic equipment.
The objectives of this experiment are twofold:
In this experiment, the hydrostatic force and center of pressure acting on a vertical surface will be determined by increasing the water depth in the apparatus water tank and by reaching an equilibrium condition between the moments acting on the balance arm of the test apparatus. The forces which create these moments are the weight applied to the balance arm and the hydrostatic force on the vertical surface.
Equipment required to carry out this experiment is the following:
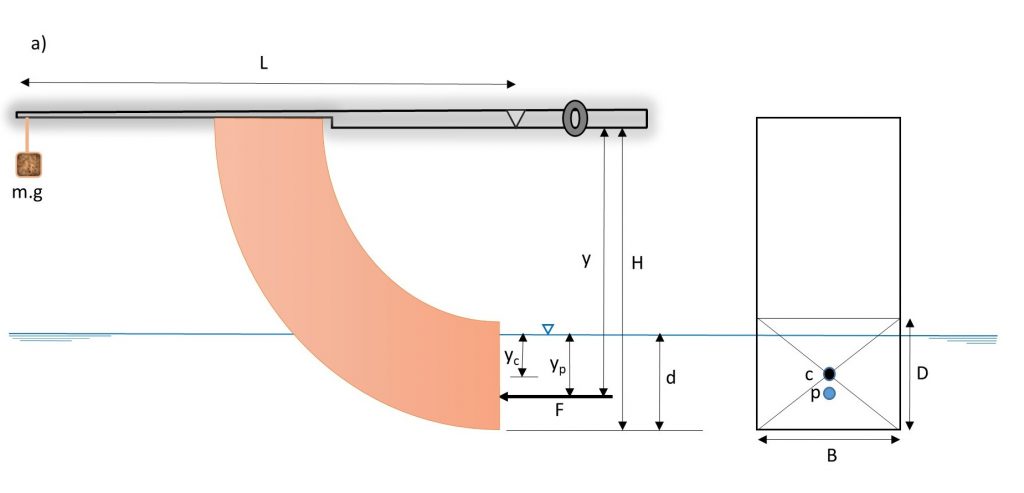
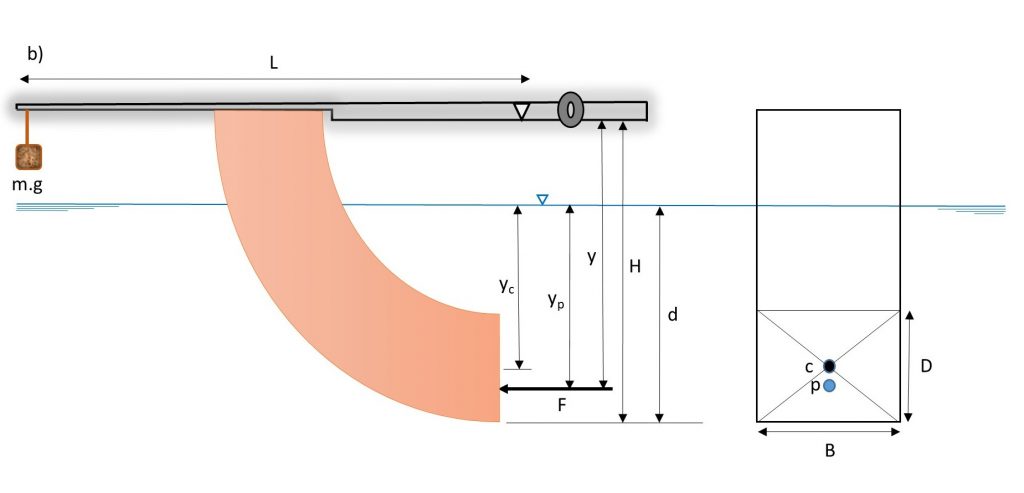
The equipment is comprised of a rectangular transparent water tank, a fabricated quadrant, a balance arm, an adjustable counter-balance weight, and a water-level measuring device (Figure 1.1).
The water tank has a drain valve at one end and three adjustable screwed-in feet on its base for leveling the apparatus. The quadrant is mounted on a balance arm that pivots on knife edges. The knife edges coincide with the center of the arc of the quadrant; therefore, the only hydrostatic force acting on the vertical surface of the quadrant creates moment about the pivot point. This moment can be counterbalanced by adding weight to the weight hanger, which is located at the left end of the balance arm, at a fixed distance from the pivot. Since the line of actions of hydrostatic forces applied on the curved surfaces passes through the pivot point, the forces have no effect on the moment. The hydrostatic force and its line of action (center of pressure) can be determined for different water depths, with the quadrant’s vertical face either partially or fully submerged.
A level indicator attached to the side of the tank shows when the balance arm is horizontal. Water is admitted to the top of the tank by a flexible tube and may be drained through a cock in the side of the tank. The water level is indicated on a scale on the side of the quadrant [1].

In this experiment, when the quadrant is immersed by adding water to the tank, the hydrostatic force applied to the vertical surface of the quadrant can be determined by considering the following [1]:
where:
m : mass on the weight hanger,
L : length of the balance arm (Figure 1.2)
F : Hydrostatic force, and
y : distance between the pivot and the center of pressure (Figure 1.2).
Then, calculated hydrostatic force and center of pressure on the vertical face of the quadrant can be compared with the experimental results.
The magnitude of the resultant hydrostatic force (F) applied to an immersed surface is given by:
where:
Pc : pressure at centroid of the immersed surface,
A: area of the immersed surface,
yc : centroid of the immersed surface measured from the water surface,
: density of fluid, and
g : acceleration due to gravity.
The hydrostatic force acting on the vertical face of the quadrant can be calculated as:
where:
B : width of the quadrant face,
d : depth of water from the base of the quadrant, and
D : height of the quadrant face.
The center of pressure is calculated as:
is the 2nd moment of area of immersed body about an axis in the free surface. By use of the parallel axes theorem:
where is the depth of the centroid of the immersed surface, and
is the 2nd moment of area of immersed body about the centroidal axis.
is calculated as:
The depth of the center of pressure below the pivot point is given by:
in which H is the vertical distance between the pivot and the base of the quadrant.
Substitution of Equation (6a and 6b) and into (4) and then into (7) yields the theoretical results, as follows:
For equilibrium of the experimental apparatus, moments about the pivot are given by Equation (1). By substitution of the derived hydrostatic force, F from Equation (3a and b), we have:
Begin the experiment by measuring the dimensions of the quadrant vertical endface (B and D) and the distances (H and L), and then perform the experiment by taking the following steps:
Please visit this link for accessing the excel workbook for this experiment.
Record the following dimensions:
All mass and water depth readings should be recorded in the Raw Data Table:
| Test No. | Mass, m (kg) | Depth of Immersion, d (m) | |
| Partially submerged | 1 | ||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 | |||
| Fully Submerged | 6 | ||
| 7 | |||
| 8 | |||
| 9 | |||
| 10 | |||
Calculate the following for the partially and fully submerged quadrants, and record them in the Result Table:
| Test No. | Mass m(kg) | Depth of immersion d(m) | Hydrostatic force F(N) | Theoretical depth of center of pressure (m) | Experimental depth of center of pressure (m) |
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 7 | |||||
| 8 | |||||
| 9 | |||||
| 10 |
Use the template provided to prepare your lab report for this experiment. Your report should include the following:
2
Energy presents in the form of pressure, velocity, and elevation in fluids with no energy exchange due to viscous dissipation, heat transfer, or shaft work (pump or some other device). The relationship among these three forms of energy was first stated by Daniel Bernoulli (1700-1782), based upon the conservation of energy principle. Bernoulli’s theorem pertaining to a flow streamline is based on three assumptions: steady flow, incompressible fluid, and no losses from the fluid friction. The validity of Bernoulli’s equation will be examined in this experiment.
Bernoulli’s theorem provides a mathematical means to understanding the mechanics of fluids. It has many real-world applications, ranging from understanding the aerodynamics of an airplane; calculating wind load on buildings; designing water supply and sewer networks; measuring flow using devices such as weirs, Parshall flumes, and venturimeters; and estimating seepage through soil, etc. Although the expression for Bernoulli’s theorem is simple, the principle involved in the equation plays vital roles in the technological advancements designed to improve the quality of human life.
The objective of this experiment is to investigate the validity of the Bernoulli equation when it is applied to a steady flow of water through a tapered duct.
In this experiment, the validity of Bernoulli’s equation will be verified with the use of a tapered duct (venturi system) connected with manometers to measure the pressure head and total head at known points along the flow.
The following equipment is required to complete the demonstration of the Bernoulli equation experiment:
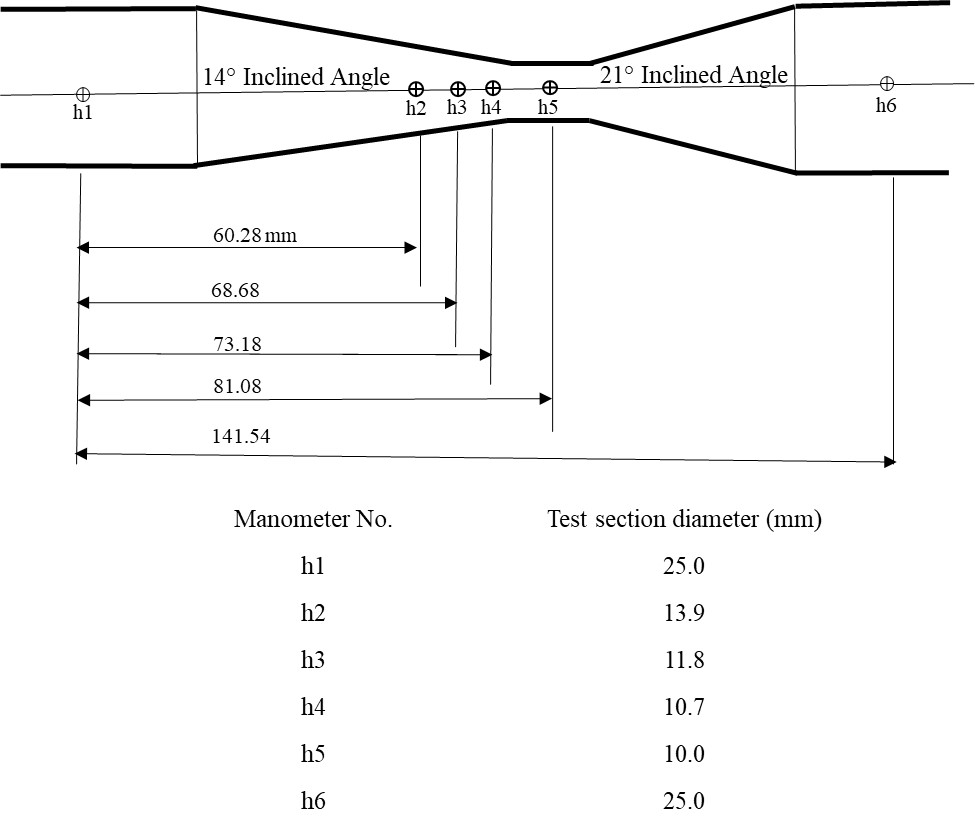
The Bernoulli test apparatus consists of a tapered duct (venturi), a series of manometers tapped into the venturi to measure the pressure head, and a hypodermic probe that can be traversed along the center of the test section to measure the total head. The test section is a circular duct of varying diameter with a 14° inclined angle on one side and a 21° inclined angle on other side. Series of side hole pressure tappings are provided to connect manometers to the test section (Figure 2.1).

Manometers allow the simultaneous measurement of the pressure heads at all of the six sections along the duct. The dimensions of the test section, the tapping positions, and the test section diameters are shown in Figure 2.2. The test section incorporates two unions, one at either end, to facilitate reversal for convergent or divergent testing. A probe is provided to measure the total pressure head along the test section by positioning it at any section of the duct. This probe may be moved after slackening the gland nut, which should be re-tightened by hand. To prevent damage, the probe should be fully inserted during transport/storage. The pressure tappings are connected to manometers that are mounted on a baseboard. The flow through the test section can be adjusted by the apparatus control valve or the bench control valve [2].
Bernoulli’s theorem assumes that the flow is frictionless, steady, and incompressible. These assumptions are also based on the laws of conservation of mass and energy. Thus, the input mass and energy for a given control volume are equal to the output mass and energy:
These two laws and the definition of work and pressure are the basis for Bernoulli’s theorem and can be expressed as follows for any two points located on the same streamline in the flow:
where:
P: pressure,
g: acceleration due to gravity,
v: fluid velocity, and
z: vertical elevation of the fluid.
In this experiment, since the duct is horizontal, the difference in height can be disregarded, i.e., z1=z2
The hydrostatic pressure (P) along the flow is measured by manometers tapped into the duct. The pressure head (h), thus, is calculated as:
Therefore, Bernoulli’s equation for the test section can be written as:
in which is called the velocity head (hd).
The total head (ht) may be measured by the traversing hypodermic probe. This probe is inserted into the duct with its end-hole facing the flow so that the flow becomes stagnant locally at this end; thus:
The conservation of energy or the Bernoulli’s equation can be expressed as:
The flow velocity is measured by collecting a volume of the fluid (V) over a time period (t). The flow rate is calculated as:
The velocity of flow at any section of the duct with a cross-sectional area of is determined as:
For an incompressible fluid, conservation of mass through the test section should be also satisfied (Equation 1a), i.e.:
If needed, the manometer levels can be adjusted by using an air pump to pressurize them. This can be accomplished by attaching the hand pump tube to the air bleed valve, opening the screw, and pumping air into the manometers. Close the screw, after pumping, to retain the pressure in the system.
Please visit this link for accessing excel workbook for this experiment.
Enter the test results into the Raw Data Tables.
| Position 1: Tapering 14° to 21° | ||||
| Test Section | Volume (Litre) | Time (sec) | Pressure Head (mm) | Total Head (mm) |
| h1 | ||||
| h2 | ||||
| h3 | ||||
| h4 | ||||
| h5 | ||||
| h6 | ||||
| h1 | ||||
| h2 | ||||
| h3 | ||||
| h4 | ||||
| h5 | ||||
| h6 | ||||
| h1 | ||||
| h2 | ||||
| h3 | ||||
| h4 | ||||
| h5 | ||||
| h6 | ||||
| Position 2: Tapering 21° to 14° | ||||
| Test Section | Volume (Litre) | Time (sec) | Pressure Head (mm) | Total Head (mm) |
| h1 | ||||
| h2 | ||||
| h3 | ||||
| h4 | ||||
| h5 | ||||
| h6 | ||||
| h1 | ||||
| h2 | ||||
| h3 | ||||
| h4 | ||||
| h5 | ||||
| h6 | ||||
| h1 | ||||
| h2 | ||||
| h3 | ||||
| h4 | ||||
| h5 | ||||
| h6 | ||||
For each set of measurements, calculate the flow rate; flow velocity, velocity head, and total head, (pressure head+ velocity head). Record your calculations in the Result Table.
| Position 1: Tapering 14° to 21° | |||||||||
| Test No. | Test Section | Distance into duct (m) | Flow Area (m²) | Flow Rate (m³/s) | Velocity (m/s) | Pressure Head (m) | Velocity Head (m) | Calculated Total Head (m) | Measured Total Head (m) |
| 1 | h1 | 0 | 0.00049 | ||||||
| h2 | 0.06028 | 0.00015 | |||||||
| h3 | 0.06868 | 0.00011 | |||||||
| h4 | 0.07318 | 0.00009 | |||||||
| h5 | 0.08108 | 0.000079 | |||||||
| h6 | 0.14154 | 0.00049 | |||||||
| 2 | h1 | 0 | 0.00049 | ||||||
| h2 | 0.06028 | 0.00015 | |||||||
| h3 | 0.06868 | 0.00011 | |||||||
| h4 | 0.07318 | 0.00009 | |||||||
| h5 | 0.08108 | 0.000079 | |||||||
| h6 | 0.14154 | 0.00049 | |||||||
| 3 | h1 | 0 | 0.00049 | ||||||
| h2 | 0.06028 | 0.00015 | |||||||
| h3 | 0.06868 | 0.00011 | |||||||
| h4 | 0.07318 | 0.00009 | |||||||
| h5 | 0.08108 | 0.000079 | |||||||
| h6 | 0.14154 | 0.00049 | |||||||
| Position 2: Tapering 21° to 14° | |||||||||
| Test No. | Test Section | Distance into duct (m) | Flow Area (m²) | Flow Rate (m³/s) | Velocity (m/s) | Pressure Head (m) | Velocity Head (m) | Calculated Total Head (m) | Measured Total Head (m) |
| 1 | h1 | 0 | 0.00049 | ||||||
| h2 | 0.06028 | 0.00015 | |||||||
| h3 | 0.06868 | 0.00011 | |||||||
| h4 | 0.07318 | 0.00009 | |||||||
| h5 | 0.08108 | 0.000079 | |||||||
| h6 | 0.14154 | 0.00049 | |||||||
| 2 | h1 | 0 | 0.00049 | ||||||
| h2 | 0.06028 | 0.00015 | |||||||
| h3 | 0.06868 | 0.00011 | |||||||
| h4 | 0.07318 | 0.00009 | |||||||
| h5 | 0.08108 | 0.000079 | |||||||
| h6 | 0.14154 | 0.00049 | |||||||
| 3 | h1 | 0 | 0.00049 | ||||||
| h2 | 0.06028 | 0.00015 | |||||||
| h3 | 0.06868 | 0.00011 | |||||||
| h4 | 0.07318 | 0.00009 | |||||||
| h5 | 0.08108 | 0.000079 | |||||||
| h6 | 0.14154 | 0.00049 | |||||||
Use the template provided to prepare your lab report for this experiment. Your report should include the following:
3
Two types of energy loss predominate in fluid flow through a pipe network; major losses, and minor losses. Major losses are associated with frictional energy loss that is caused by the viscous effects of the medium and roughness of the pipe wall. Minor losses, on the other hand, are due to pipe fittings, changes in the flow direction, and changes in the flow area. Due to the complexity of the piping system and the number of fittings that are used, the head loss coefficient (K) is empirically derived as a quick means of calculating the minor head losses.
The term “minor losses”, used in many textbooks for head loss across fittings, can be misleading since these losses can be a large fraction of the total loss in a pipe system. In fact, in a pipe system with many fittings and valves, the minor losses can be greater than the major (friction) losses. Thus, an accurate K value for all fittings and valves in a pipe system is necessary to predict the actual head loss across the pipe system. K values assist engineers in totaling all of the minor losses by multiplying the sum of the K values by the velocity head to quickly determine the total head loss due to all fittings. Knowing the K value for each fitting enables engineers to use the proper fitting when designing an efficient piping system that can minimize the head loss and maximize the flow rate.
The objective of this experiment is to determine the loss coefficient (K) for a range of pipe fittings, including several bends, a contraction, an enlargement, and a gate valve.
The head loss coefficients are determined by measuring the pressure head differences across a number of fittings that are connected in series, over a range of steady flows, and applying the energy equation between the sections before and after each fitting.
The following equipment is required to perform the energy loss in pipe fittings experiment:
The energy loss in fittings apparatus consists of a series of fittings, a flow control valve, twelve manometers, a differential pressure gauge, and an air-bleed valve (Figure 3.1).
The fittings listed below, connected in a series configuration, will be examined for their head loss coefficient (K):

The manometers are tapped into the pipe system (one before and one after each fitting, except for the gate valve) to measure the pressure head difference caused by each fitting. The pressure difference for the valve is directly measured by the differential pressure gauge. The air-bleed valve facilitates purging the system and adjusting the water level in the manometers to a convenient level, by allowing air to enter them. Two clamps, which close off the tappings to the mitre, are introduced while experiments are being performed on the gate valve. The flow rate is controlled by the flow control valve [3].
The internal diameter of the pipe and all fittings, except for the enlargement and contraction, is 0.0183 m. The internal diameter of the pipe at the enlargement’s outlet and the contraction’s inlet is 0.0240 m.
Bernoulli’s equation can be used to evaluate the energy loss in a pipe system:
In this equation ,
, and z are pressure head, velocity head, and potential head, respectively. The total head loss, hL, includes both major and minor losses.
If the diameter through the pipe fitting is kept constant, then . Therefore, if the change in elevation head is neglected, the manometric head difference is the static head difference that is equal to the minor loss
through the fitting.
in which and
are manometer readings before and after the fitting.
The energy loss that occurs in a pipe fitting can also be expressed as a fraction (K ) of the velocity head through the fitting:
where:
K: loss coefficient, and
v: mean flow velocity into the fitting.
Because of the complexity of the flow in many fittings, K is usually determined by experiment [3]. The head loss coefficient (K) is calculated as the ratio of the manometric head difference between the input and output of the fitting to the velocity head.
Due to the change in the pipe cross-sectional area in enlargement and contraction fittings, the velocity difference cannot be neglected. Thus:
Therefore, these types of fittings experience an additional change in static pressure, i.e.:
.
This value will be negative for the contraction since and it will be positive for enlargement because
. From Equation (5), note that
will be negative for the enlargement.
The pressure difference ( ) between before and after the gate valve is measured directly using the pressure gauge. This can then be converted to an equivalent head loss by using the conversion ratio:
1 bar= 10.2 m water
The loss coefficient for the gate valve may then be calculated by using Equation (4).
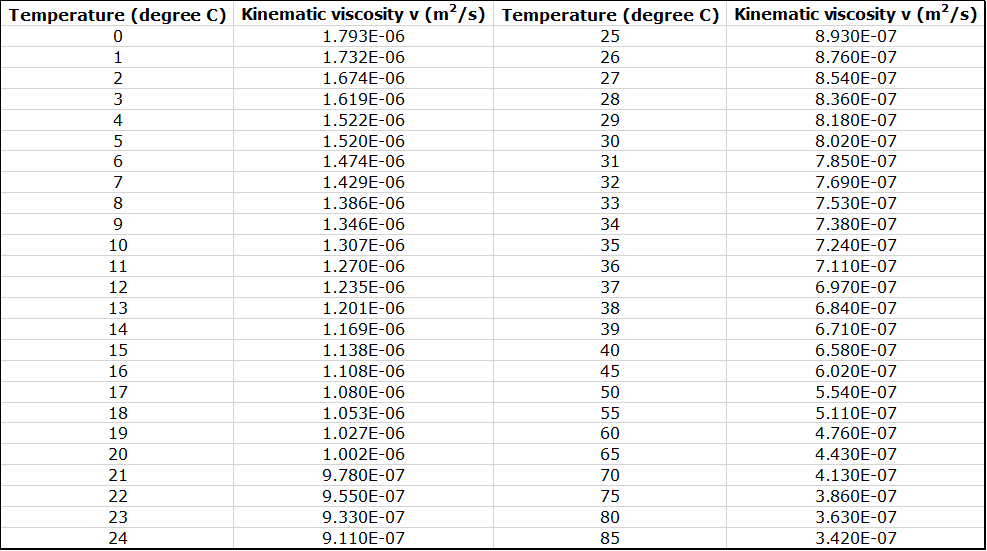
To identify the flow regime through the fitting, the Reynolds number is calculated as:
where v is the cross-sectional mean velocity, D is the pipe diameter and is the fluid kinematic viscosity (Figure 3.2).
It is not possible to measure head due to all of the fittings simultaneously; therefore, it is necessary to run two separate experiments.
In this part, head losses caused by fittings, except for the gate valve, will be measured; therefore, this valve should be kept fully open throughout Part A. The following steps should be followed for this part:
In this experiment, the head loss across the gate valve will be measured by taking the following steps:
Please visit this link for accessing excel workbook for this experiment.
Record all of the manometer and pressure gauge readings, as well as the volumetric measurements, in the Raw Data Tables.
Part A – Head Loss Across Pipe Fittings
| Test No. 1: Volume Collected (liters): | Time (s): | |
| Fitting | h1 (m) | h2 (m) |
| Enlargement | ||
| Contraction | ||
| Long Bend | ||
| Short Bend | ||
| Elbow | ||
| Mitre | ||
| Test No. 2: Volume Collected (liters): | Time (s): | |
| Enlargement | ||
| Contraction | ||
| Long Bend | ||
| Short Bend | ||
| Elbow | ||
| Mitre | ||
| Test No. 3: Volume Collected (liters): | Time (s): | |
| Enlargement | ||
| Contraction | ||
| Long Bend | ||
| Short Bend | ||
| Elbow | ||
| Mitre | ||
| Test No. 4: Volume Collected (liters): | Time (s): | |
| Enlargement | ||
| Contraction | ||
| Long Bend | ||
| Short Bend | ||
| Elbow | ||
| Mitre | ||
| Test No. 5: Volume Collected (liters): | Time (s): | |
| Enlargement | ||
| Contraction | ||
| Long Bend | ||
| Short Bend | ||
| Elbow | ||
| Mitre | ||
| Head Loss (bar) | Volume (liters) | Time (s) |
| 0.3 | ||
| 0.6 | ||
| 0.9 | ||
| Water Temperature: | ||
Calculate the values of the discharge, flow velocity, velocity head, and Reynolds number for each experiment, as well as the K values for each fitting and the gate valve. Record your calculations in the following sample Result Tables.
| Test No: | Flow Rate Q (m3/s): | Velocity v (m/s): | |||||
| Fitting | h1 (m) | h2 (m) | Corrected | v2/2g (m) | K | Reynolds Number | |
| Enlargement | |||||||
| Contraction | |||||||
| Long Bend | |||||||
| Short Bend | |||||||
| Elbow | |||||||
| Mitre | |||||||
| Head Loss | Volume (m3) | Time (s) | Flow Rate Q (m3/s) | Velocity (m/s) | v2/2g (m) | K | Reynolds Number | |
| (bar) | (m) | |||||||
| 0.3 | ||||||||
| 0.6 | ||||||||
| 0.9 | ||||||||
Use the template provided to prepare your lab report for this experiment. Your report should include the following:
4
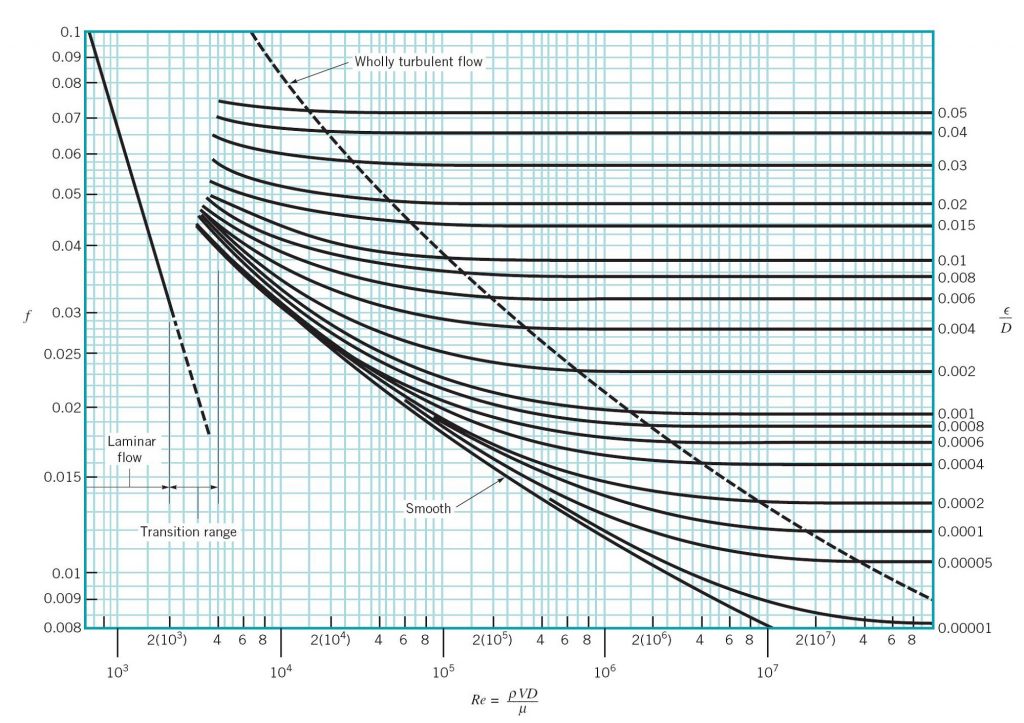
The total energy loss in a pipe system is the sum of the major and minor losses. Major losses are associated with frictional energy loss that is caused by the viscous effects of the fluid and roughness of the pipe wall. Major losses create a pressure drop along the pipe since the pressure must work to overcome the frictional resistance. The Darcy-Weisbach equation is the most widely accepted formula for determining the energy loss in pipe flow. In this equation, the friction factor (f ), a dimensionless quantity, is used to describe the friction loss in a pipe. In laminar flows, f is only a function of the Reynolds number and is independent of the surface roughness of the pipe. In fully turbulent flows, f depends on both the Reynolds number and relative roughness of the pipe wall. In engineering problems, f is determined by using the Moody diagram.
In engineering applications, it is important to increase pipe productivity, i.e. maximizing the flow rate capacity and minimizing head loss per unit length. According to the Darcy-Weisbach equation, for a given flow rate, the head loss decreases with the inverse fifth power of the pipe diameter. Doubling the diameter of a pipe results in the head loss decreasing by a factor of 32 (≈ 97% reduction), while the amount of material required per unit length of the pipe and its installation cost nearly doubles. This means that energy consumption, to overcome the frictional resistance in a pipe conveying a certain flow rate, can be significantly reduced at a relatively small capital cost.
The objective of this experiment is to investigate head loss due to friction in a pipe, and to determine the associated friction factor under a range of flow rates and flow regimes, i.e., laminar, transitional, and turbulent.
The friction factor is determined by measuring the pressure head difference between two fixed points in a straight pipe with a circular cross section for steady flows.
The following equipment is required to perform the energy loss in pipes experiment:
The pipe friction apparatus consists of a test pipe (mounted vertically on the rig), a constant head tank, a flow control valve, an air-bleed valve, and two sets of manometers to measure the head losses in the pipe (Figure 4.1). A set of two water-over-mercury manometers is used to measure large pressure differentials, and two water manometers are used to measure small pressure differentials. When not in use, the manometers may be isolated, using Hoffman clamps.
Since mercury is considered a hazardous substance, it cannot be used in undergraduate fluid mechanics labs. Therefore, for this experiment, the water-over-mercury manometers are replaced with a differential pressure gauge to directly measure large pressure differentials.
This experiment is performed under two flow conditions: high flow rates and low flow rates. For high flow rate experiments, the inlet pipe is connected directly to the bench water supply. For low flow rate experiments, the inlet to the constant head tank is connected to the bench supply, and the outlet at the base of the head tank is connected to the top of the test pipe [4].
The apparatus’ flow control valve is used to regulate flow through the test pipe. This valve should face the volumetric tank, and a short length of flexible tube should be attached to it, to prevent splashing.
The air-bleed valve facilitates purging the system and adjusting the water level in the water manometers to a convenient level, by allowing air to enter them.

The energy loss in a pipe can be determined by applying the energy equation to a section of a straight pipe with a uniform cross section:
If the pipe is horizontal:
Since vin = vout :
The pressure difference (Pout-Pin) between two points in the pipe is due to the frictional resistance, and the head loss hL is directly proportional to the pressure difference.
The head loss due to friction can be calculated from the Darcy-Weisbach equation:
where:
: head loss due to flow resistance
f: Darcy-Weisbach coefficient
L: pipe length
D: pipe diameter
v: average velocity
g: gravitational acceleration.
For laminar flow, the Darcy-Weisbach coefficient (or friction factor f ) is only a function of the Reynolds number (Re) and is independent of the surface roughness of the pipe, i.e.:
For turbulent flow, f is a function of both the Reynolds number and the pipe roughness height, . Other factors, such as roughness spacing and shape, may also affect the value of f; however, these effects are not well understood and may be negligible in many cases. Therefore, f must be determined experimentally. The Moody diagram relates f to the pipe wall relative roughness (
/D) and the Reynolds number (Figure 4.2).
Instead of using the Moody diagram, f can be determined by utilizing empirical formulas. These formulas are used in engineering applications when computer programs or spreadsheet calculation methods are employed. For turbulent flow in a smooth pipe, a well-known curve fit to the Moody diagram is given by:
Reynolds number is given by:
where v is the average velocity, D is the pipe diameter, and and
are dynamic and kinematic viscosities of the fluid, respectively. (Figure 4.3).
In this experiment, hL is measured directly by the water manometers and the differential pressure gauge that are connected by pressure tappings to the test pipe. The average velocity, v, is calculated from the volumetric flow rate (Q ) as:
The following dimensions from the test pipe may be used in the appropriate calculations [4]:
Length of test pipe = 0.50 m,
Diameter of test pipe = 0.003 m.

One or more interactive elements has been excluded from this version of the text. You can view them online here: https://uta.pressbooks.pub/appliedfluidmechanics/?p=129
The high flow rate will be supplied to the test section by connecting the equipment inlet pipe to the hydraulics bench, with the pump turned off. The following steps should be followed.
The pressure difference measured by the differential pressure gauge can be converted to an equivalent head loss (hL) by using the conversion ratio:
1 bar = 10.2 m water
The low flow rate will be supplied to the test section by connecting the hydraulics bench outlet pipe to the head tank with the pump turned off. Take the following steps.
Please use this link for accessing excel workbook for this experiment.
Record all of the manometer and pressure gauge readings, water temperature, and volumetric measurements, in the Raw Data Tables.
| Test No. | Head Loss (bar) | Volume (Liters) | Time (s) |
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 | |||
| 6 | |||
| 7 | |||
| 8 | |||
| 9 | |||
| 10 |
| Test No. | h1 (m) | h2 (m) | Head loss hL (m) | Volume (liters) | Time (s) |
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 7 | |||||
| 8 | |||||
| Water Temperature: | |||||
Calculate the values of the discharge; average flow velocity; and experimental friction factor, f using Equation 3, and the Reynolds number for each experiment. Also, calculate the theoretical friction factor, f, using Equation 4 for laminar flow and Equation 5 for turbulent flow for a range of Reynolds numbers. Record your calculations in the following sample Result Tables.
| Test No. | Head loss hL (m) | Volume (liters) | Time (s) | Discharge (m3/s) | Velocity (m/s) | Friction Factor, f | Reynolds Number |
| 1 | |||||||
| 2 | |||||||
| 3 | |||||||
| 4 | |||||||
| 5 | |||||||
| 6 | |||||||
| 7 | |||||||
| 8 | |||||||
| 9 | |||||||
| 10 | |||||||
| 11 | |||||||
| 12 | |||||||
| 13 | |||||||
| 14 | |||||||
| 15 | |||||||
| 16 | |||||||
| 17 | |||||||
| 18 |
| No. | Flow Regime | Reynolds Number | Friction Factor, f |
| 1 | Laminar (Equation 4) | 100 | |
| 2 | 200 | ||
| 3 | 400 | ||
| 4 | 800 | ||
| 5 | 1600 | ||
| 6 | 2000 | ||
| 7 | Turbulent (Equation 5) | 4000 | |
| 8 | 6000 | ||
| 9 | 8000 | ||
| 10 | 10000 | ||
| 11 | 12000 | ||
| 12 | 16000 | ||
| 13 | 20000 |
Use the template provided to prepare your lab report for this experiment. Your report should include the following:
5
Moving fluid, in natural or artificial systems, may exert forces on objects in contact with it. To analyze fluid motion, a finite region of the fluid (control volume) is usually selected, and the gross effects of the flow, such as its force or torque on an object, is determined by calculating the net mass rate that flows into and out of the control volume. These forces can be determined, as in solid mechanics, by the use of Newton’s second law, or by the momentum equation. The force exerted by a jet of fluid on a flat or curve surface can be resolved by applying the momentum equation. The study of these forces is essential to the study of fluid mechanics and hydraulic machinery.
Engineers and designers use the momentum equation to accurately calculate the force that moving fluid may exert on a solid body. For example, in hydropower plants, turbines are utilized to generate electricity. Turbines rotate due to force exerted by one or more water jets that are directed tangentially onto the turbine’s vanes or buckets. The impact of the water on the vanes generates a torque on the wheel, causing it to rotate and to generate electricity.
The objective of this experiment is to investigate the reaction forces produced by the change in momentum of a fluid flow when a jet of water strikes a flat plate or a curved surface, and to compare the results from this experiment with the computed forces by applying the momentum equation.
The momentum force is determined by measuring the forces produced by a jet of water impinging on solid flat and curved surfaces, which deflect the jet at different angles.
The following equipment is required to perform the impact of the jet experiment:
The jet apparatus is a clear acrylic cylinder, a nozzle, and a flow deflector (Figure 5.1). Water enters vertically from the top of the cylinder, through a nozzle striking a target, mounted on a stem, and leaves through the outlet holes in the base of the cylinder. An air vent at the top of the cylinder maintains the atmospheric pressure inside the cylinder. A weight pan is mounted at the top of the stem to allow the force of the striking water to be counterbalanced by applied masses [5].

The velocity of the water (v) leaving the nozzle with the cross-sectional area (A) can be calculated by:
in which Q is the flow rate.
Applying the energy equation between the nozzle exit point and the surface of the deflector shows that the magnitude of the flow velocity does not change as the water flows around the deflector; only the direction of the flow changes.
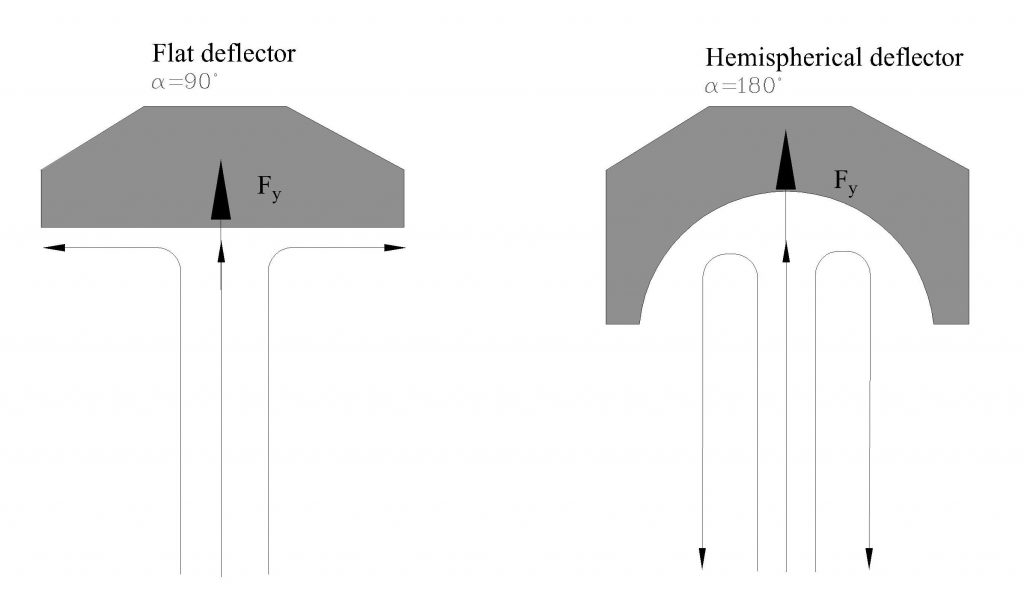
Applying the momentum equation to a control volume encompassing the deflected flow results in:
where:
Fy: force exerted by the deflector on the fluid
: fluid density
: 180-
, where
is the flow deflection angle (Figure 5.2).
From equilibrium of forces in a vertical direction, Fy is balanced by the applied weight on the weight pan, W (W = mg, where m is the applied mass), i.e., Fy = W. Therefore:
Since Q = vA, this equation can be written as:
Perform the experiment by taking the following steps:
Please use this link for accessing excel workbook for this experiment.
Use the following tables to record your measurements.
| Test No. | Deflection Angles (degree) | ||||||||
| 90 | 120 | 180 | |||||||
| Volume (Liter) | Time (s) | Applied Mass (kg) | Volume (Liter) | Time (s) | Applied Mass (kg) | Volume (Liter) | Time (s) | Applied Mass (kg) | |
| 1 | |||||||||
| 2 | |||||||||
| 3 | |||||||||
| 4 | |||||||||
| 5 | |||||||||
| 6 | |||||||||
| 7 | |||||||||
| 8 | |||||||||
| 9 | |||||||||
| 10 | |||||||||
The nozzle should be of the following dimensions.
These values may be measured as part of the experimental procedure and replaced with the above dimensions.
For each set of measurements, calculate the applied weight (W), flow rate (Q), velocity squared (v2), force (Fy ), and theoretical and experimental slope (S) of the relationship between W and v2. The theoretical slope is determined from Equation 5, as follows:
The experimental value of S is obtained from a graph W of plotted against v2.
| Nozzle Diameter (m)= | Flow Area (m2) = | Deflector Angle (degree)= | |||||
| Test No. | Applied Weight (N) | Flow Rate (m3/s) | Velocity (m/s) | Velocity2 (m/s)2 | Force (N) | Theoretical Slope | Experimental Slope |
| 1 | |||||||
| 2 | |||||||
| 3 | |||||||
| 4 | |||||||
| 5 | |||||||
| 6 | |||||||
| 7 | |||||||
| 8 | |||||||
| 9 | |||||||
| 10 | |||||||
Use the template provided to prepare your lab report for this experiment. Your report should include the following:
6
An orifice is an opening, of any size or shape, in a pipe or at the bottom or side wall of a container (water tank, reservoir, etc.), through which fluid is discharged. If the geometric properties of the orifice and the inherent properties of the fluid are known, the orifice can be used to measure flow rates. Flow measurement by an orifice is based on the application of Bernoulli’s equation, which states that a relationship exists between the pressure of the fluid and its velocity. The flow velocity and discharge calculated based on the Bernoulli’s equation should be corrected to include the effects of energy loss and viscosity. Therefore, for accurate results, the coefficient of velocity (Cv) and the coefficient of discharge (Cd) should be calculated for an orifice. This experiment is being conducted to calibrate the coefficients of the given orifices in the lab.
Orifices have many applications in engineering practice besides the metering of fluid flow in pipes and reservoirs. Flow entering a culvert or storm drain inlet may act as orifice flow; the bottom outlet of a dam is another example. The coefficients of velocity and discharge are necessary to accurately predict flow rates from orifices.
The objective of this lab experiment is to determine the coefficients of velocity and discharge of two small orifices in the lab and compare them with values in textbooks and other reliable sources.
The coefficients of velocity and discharge are determined by measuring the trajectory of a jet issuing fluid from an orifice in the side of a reservoir under steady flow conditions, i.e., a constant reservoir head.
The following equipment is required to perform the orifice and free jet flow experiment:
The orifice and free jet flow apparatus consists of a cylindrical head tank with an orifice plate set into its side (Figure 6.1). An adjustable overflow pipe is adjacent to the head tank to allow changes in the water level. A flexible hose attached to the overflow pipe returns excess water to the hydraulics bench. A scale attached to the head tank indicates the water level. A baffle at the base of the head tank promotes smooth flow conditions inside the tank, behind the orifice plate. Two orifice plates with 3 and 6 mm diameters are provided and may be interchanged by slackening the two thumb nuts. The trajectory of the jet may be measured, using the vertical needles. For this purpose, a sheet of paper should be attached to the backboard, and the needles should be adjusted to follow the trajectory of the water jet. The needles may be locked, using a screw on the mounting bar. The positions of the tops of the needles can be marked to plot the trajectory. A drain plug in the base of the head tank allows water to be drained from the equipment at the end of the experiment [6].

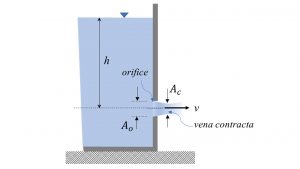
The orifice outflow velocity can be calculated by applying Bernoulli’s equation (for a steady, incompressible, frictionless flow) to a large reservoir with an opening (orifice) on its side (Figure 6.2):
where h is the height of fluid above the orifice. This is the ideal velocity since the effect of fluid viscosity is not considered in deriving Equation 1. The actual flow velocity, however, is smaller than vi and is calculated as:
Cv is the coefficient of velocity, which allows for the effects of viscosity; therefore, Cv <1. The actual outflow velocity calculated by Equation (2) is the velocity at the vena contracta, where the diameter of the jet is the least and the flow velocity is at its maximum (Figure 6.2).
The actual outflow rate may be calculated as:
where Ac is the flow area at the vena contracta. Ac is smaller than the orifice area, Ao (Figure 6.2), and is given by:
where Cc is the coefficient of contraction; therefore, Cc < 1.
Substituting v and Ac from Equations 2 and 4 into Equation 3 results in:
The product CvCc is called the coefficient of discharge, Cd; Thus, Equation 5 can be written as:
The coefficient of velocity, Cv, and coefficient of discharge, Cd, are determined experimentally as follows.
If the effect of air resistance on the jet leaving the orifice is neglected, the horizontal component of the jet velocity can be assumed to remain constant. Therefore, the horizontal distance traveled by jet (x) in time (t) is equal to:
The vertical component of the trajectory of the jet will have a constant acceleration downward due to the force of gravity. Therefore, at any time, t, the y-position of the jet may be calculated as:
Rearranging Equation (8) gives:
Substitution of t and v from Equations 9 and 2 into Equation 7 results in:
Equations (10) can be rearranged to find Cv:
Therefore, for steady flow conditions (i.e., constant h in the head tank), the value of Cv can be determined from the x, y coordinates of the jet trajectory. A graph of x plotted against will have a slope of 2Cv.
If Cd is assumed to be constant, then a graph of Q plotted against (Equation 6) will be linear, and the slope of this graph will be:
This experiment will be performed in two parts. Part A is performed to determine the coefficient of velocity, and Part B is conducted to determine the coefficient of discharge.
Set up the equipment as follows:
Repeat the above procedure for the second orifice with diameter of 6 mm.
The procedure should also be repeated for the second orifice.
Please visit this link for accessing excel workbook for this experiment.
Use the following tables to record your measurements.
| Needle No. | Orifice Diameter (m) | x (m) | Head (m) | y(m) | ||||
| Trial 1 | Trial 2 | Trial 3 | Trial 1 | Trial 2 | Trial 3 | |||
| 1 | 0.003 | 0.014 | ||||||
| 2 | 0.064 | |||||||
| 3 | 0.114 | |||||||
| 4 | 0.164 | |||||||
| 5 | 0.214 | |||||||
| 6 | 0.264 | |||||||
| 7 | 0.314 | |||||||
| 8 | 0.364 | |||||||
| Needle No. | Orifice Diameter (m) | x (m) | Head (m) | y(m) | ||||
| Trial 1 | Trial 2 | Trial 3 | Trial 1 | Trial 2 | Trial 3 | |||
| 1 | 0.006 | 0.014 | ||||||
| 2 | 0.064 | |||||||
| 3 | 0.114 | |||||||
| 4 | 0.164 | |||||||
| 5 | 0.214 | |||||||
| 6 | 0.264 | |||||||
| 7 | 0.314 | |||||||
| 8 | 0.364 | |||||||
Test | Orifice Diameter (m) | Head (m) | Volume (L) | Time (s) |
| 1 | 0.003 | |||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 6 | 0.006 | |||
| 7 | ||||
| 8 | ||||
| 9 | ||||
| 10 |
Calculate the values of (y.h)1/2 for Part A and discharge (Q) and (h0.5) for Part B. Record your calculations in the following Result Tables.
The following dimensions of the equipment are used in the appropriate calculations. If necessary, these values may be checked as part of the experimental procedure and replaced with your measurements [6].
– Diameter of the small orifice: 0.003 m
– Diameter of the large orifice: 0.006 m
– Pitch of needles: 0.05 m
| Needle No. | Orifice Diameter (m) | x (m) | Head (m) | y(m) | (y.h)1/2(m) | ||||||
| Trial 1 | Trial 2 | Trial 3 | Trial 1 | Trial 2 | Trial 3 | Trial 1 | Trial 2 | Trial 3 | |||
| 1 | 0.003 | 0.014 | |||||||||
| 2 | 0.064 | ||||||||||
| 3 | 0.114 | ||||||||||
| 4 | 0.164 | ||||||||||
| 5 | 0.214 | ||||||||||
| 6 | 0.264 | ||||||||||
| 7 | 0.314 | ||||||||||
| 8 | 0.364 | ||||||||||
| Needle No. | Orifice Diameter (m) | x (m) | Head (m) | y(m) | (y.h)1/2(m) | ||||||
| Trial 1 | Trial 2 | Trial 3 | Trial 1 | Trial 2 | Trial 3 | Trial 1 | Trial 2 | Trial 3 | |||
| 1 | 0.006 | 0.014 | |||||||||
| 2 | 0.064 | ||||||||||
| 3 | 0.114 | ||||||||||
| 4 | 0.164 | ||||||||||
| 5 | 0.214 | ||||||||||
| 6 | 0.264 | ||||||||||
| 7 | 0.314 | ||||||||||
| 8 | 0.364 | ||||||||||
Test | Orifice Diameter (m) | Head (m) | Volume (L) | Time (s) | Volume (m3) | Q (m3/sec) | h0.5 (m0.5) |
| 1 | 0.003 | ||||||
| 2 | |||||||
| 3 | |||||||
| 4 | |||||||
| 5 | |||||||
| 6 | 0.006 | ||||||
| 7 | |||||||
| 8 | |||||||
| 9 | |||||||
| 10 |
Use the template provided to prepare your lab report for this experiment. Your report should include the following:
Part A: On one chart, plot a graph of x values (y-axis) against (y.h)1/2 values (x-axis) for each test. Calculate the slope of these graphs, using the equation of the best-fit for your experimental data and by setting the intercept to zero. Using Equation 11, calculate the coefficient of velocity for each orifice as:
Part B: Plot Q values (y-axis) against (h)0.5 values (x-axis). Determine the slope of this graph, using the equation of the best- fit for your experimental data and by setting the intercept to zero. Based on Equation 12, calculate the coefficient of discharge for each orifice, using the equation of the best-fit for your experimental data and the following relationship:
7
In nature and in laboratory experiments, flow may occur under two very different regimes: laminar and turbulent. In laminar flows, fluid particles move in layers, sliding over each other, causing a small energy exchange to occur between layers. Laminar flow occurs in fluids with high viscosity, moving at slow velocity. The turbulent flow, on the other hand, is characterized by random movements and intermixing of fluid particles, with a great exchange of energy throughout the fluid. This type of flow occurs in fluids with low viscosity and high velocity. The dimensionless Reynolds number is used to classify the state of flow. The Reynolds Number Demonstration is a classic experiment, based on visualizing flow behavior by slowly and steadily injecting dye into a pipe. This experiment was first performed by Osborne Reynolds in the late nineteenth century.
The Reynolds number has many practical applications, as it provides engineers with immediate information about the state of flow throughout pipes, streams, and soils, helping them apply the proper relationships to solve the problem at hand. It is also very useful for dimensional analysis and similitude. As an example, if forces acting on a ship need to be studied in the laboratory for design purposes, the Reynolds number of the flow acting on the model in the lab and on the prototype in the field should be the same.
The objective of this lab experiment is to illustrate laminar, transitional, and fully turbulent flows in a pipe, and to determine under which conditions each flow regime occurs.
The visualization of flow behavior will be performed by slowly and steadily injecting dye into a pipe. The state of the flow (laminar, transitional, and turbulent) will be visually determined and compared with the results from the calculation of the Reynolds number.
The following equipment is required to perform the Reynolds number experiment:
The equipment includes a vertical head tank that provides a constant head of water through a bellmouth entry to the flow visualization glass pipe. Stilling media (marbles) are placed inside the tank to tranquilize the flow of water entering the pipe. The discharge through this pipe is regulated by a control valve and can be measured using a measuring cylinder [7]. The flow velocity, therefore, can be determined to calculate Reynolds number. A dye reservoir is mounted on top of the head tank, from which a blue dye can be injected into the water to enable observation of flow conditions (Figure 7.1).

Flow behavior in natural or artificial systems depends on which forces (inertia, viscous, gravity, surface tension, etc.) predominate. In slow-moving laminar flows, viscous forces are dominant, and the fluid behaves as if the layers are sliding over each other. In turbulent flows, the flow behavior is chaotic and changes dramatically, since the inertial forces are more significant than the viscous forces.
In this experiment, the dye injected into a laminar flow will form a clear well-defined line. It will mix with the water only minimally, due to molecular diffusion. When the flow in the pipe is turbulent, the dye will rapidly mix with the water, due to the substantial lateral movement and energy exchange in the flow. There is also a transitional stage between laminar and turbulent flows, in which the dye stream will wander about and show intermittent bursts of mixing, followed by a more laminar behavior.
The Reynolds number (Re), provides a useful way of characterizing the flow. It is defined as:
where () is the kinematic viscosity of the water (Figure 7.2), v is the mean flow velocity and d is the diameter of the pipe.
The Reynolds number is a dimensionless parameter that is the ratio of the inertial (destabilizing) force to the viscosity (stabilizing) force. As Re increases, the inertial force becomes relatively larger, and the flow destabilizes and becomes fully turbulent.
The Reynolds experiment determines the critical Reynolds number for pipe flow at which laminar flow (Re<2000 ) becomes transitional (2000<Re<4000 ) and the transitional flow becomes turbulent (Re>4000). The advantage of using a critical Reynolds number, instead of critical velocity, is that the results of the experiments are applicable to all Newtonian fluid flows in pipes with a circular cross-section.

Set up the equipment as follows:
Note that any movement of the outflow tube during a test will cause changes in the flow rate, since it is driven by the height difference between the head tank surface and the outflow point.
Note that at intermediate flows, it is possible to have a laminar characteristic in the upper part of the test section, which develops into transitional flow lower down. This upper section behavior is described as an “inlet length flow,” which means that the boundary layer has not yet extended across the pipe radius.
Please visit this link for accessing excel workbook for this experiment.
The following dimensions of the equipment are used in the appropriate calculations. If required, measure them to make sure that they are accurate [7].
Use the following table to record your measurements and observations.
| Observed Flow Regime | Volume (L) | Time (sec) | Temperature ( |
Calculate discharge, flow velocity, and Reynolds number ( Re). Classify the flow based on the Re of each experiment. Record your calculations in the following table.
| Observed Flow Regime | Discharge Q(m3/sec) | Velocity v(m/sec) | Kinematic Viscosity v(m2/s) | Renolds Number | Flow Regime Classified using Reynolds Number |
Use the template provided to prepare your lab report for this experiment. Your report should include the following:
8
Vortices can occur naturally or be produced in a laboratory. There are two types of vortices: free vortices and forced vortices. A free vortex is formed, for example, when water flows out of a vessel through a central hole in the base. No external force is required to rotate the fluid, and the degree of rotation is dependent upon the initial disturbance. Whirlpools in rivers and tornadoes are examples of natural free vortices. A forced vortex, on the other hand, is caused by external forces on the fluid. It can be created by rotating a vessel containing fluid or by paddling in fluid. Rotational flow created by impellers of a pump is an example of a forced vortex in turbomachinery.
Studying natural phenomena such as hurricanes, tornadoes, and whirlpools (free vortices) requires a full understanding of vortex behavior. It is also critical for engineers and designers to be able to characterize forced vortices generated in machinery, such as centrifugal pumps or turbines. Vortices often have adverse effects, as have been seen during hurricanes, tornadoes, or scour holes created downstream of a dam outlet; however, understanding vortex behavior has enabled engineers to design turbomachinery and hydraulic structures that take advantage of these phenomena. For example, hydrodynamic separators have been developed, based on vortex behavior (swirling flow), to separate solid materials from liquids. This type of separator is used in water treatment plants.
The objective of this lab experiment is to study and compare the water surface profiles of free and forced vortices.
This experiment is performed by measuring the water surface profiles of a number of free and forced vortices, and observing the differences. We will study the profiles of free vortices that are produced when water flows from orifices of different diameters that are installed at the base of a tank. Varying the size of the orifice creates changes in the flow rate, thereby changing the rotational speed and size of the vortex profile. Forced vortices are created due to external forces, so we will increase the rotational speed throughout the experiment to study the theoretical and experimental relationships between the vortex surface profile and angular velocity.
The following equipment is required to perform the free and forced experiment:
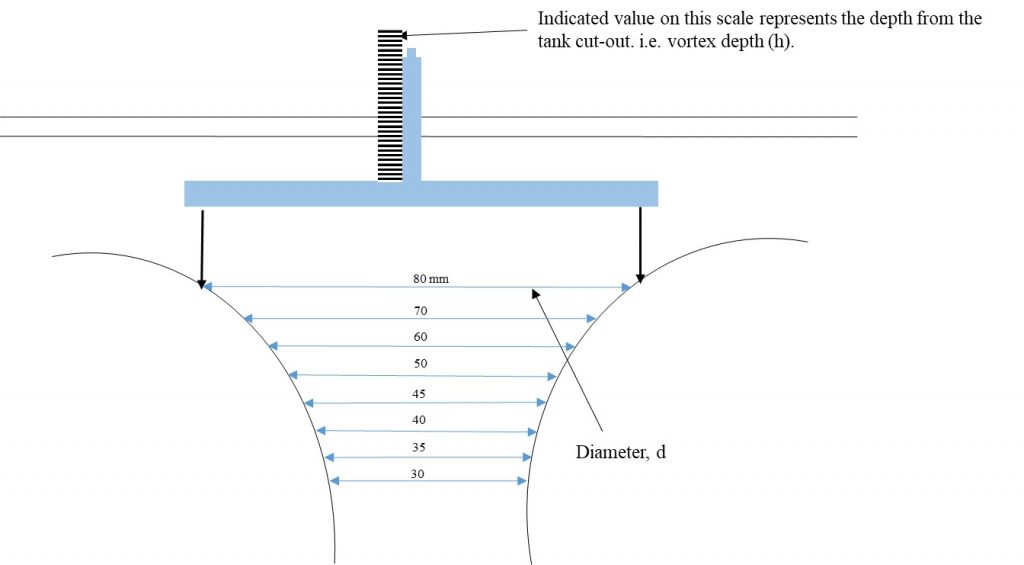
The free and forced vortices apparatus consists of a transparent cylindrical vessel, 250 mm in diameter and 180 mm deep, with two pairs of diametrically opposed inlet tubes of 9.0 mm and 12.5 mm diameter. The 12.5 diameter inlet tubes are angled at 15° to the diameter in order to create a swirling motion of the water entering the vessel during the free vortex experiment (Figure 8.1a). An outlet is centrally positioned in the base of the vessel, and a set of push-in orifices of 8, 16, and 24 mm diameter (Figure 8.1b) is supplied to reduce the outlet diameter to a suitable value and produce free vortices of different sizes. The vortex surface profile is determined by a measuring caliper (Figure 8.1c) housed on a mounted bridge, that measures the diameter of the vortex at various elevations. This provides the coordinate points that are required for plotting the free vortex profile [8].
The forced vortex is created by positioning a bushed plug in the central hole of the vessel and introducing the flow through 9 mm inlet tubes that are angled at 60° to the diameter. The water inflow from these tubes impinges on a two-blade paddle. The water exits the vessel via the 12.5 mm angled inlet tubes that are used as entry tubes for the free vortex experiment. The two-bladed paddle rotates on a vertical shaft supported by the bushed plug. A bridge piece mounted on top of the vessel houses a series of needles (Figure 8.1d) to determine the coordinates of the forced vortex profile [8].
A 3-way valve allows water to be diverted through the 12.5 mm inlet tubes for the free vortex experiment, and 9 mm inlet tubes for the forced vortex experiment.

Two types of vortices are distinguished in the dynamics of the motion: forced and free vortices. The forced vortex is caused by external forces on the fluid, such as the impeller of a pump, and the free vortex naturally occurs in the flow and can be observed in a drain or in the atmosphere of a tornado.
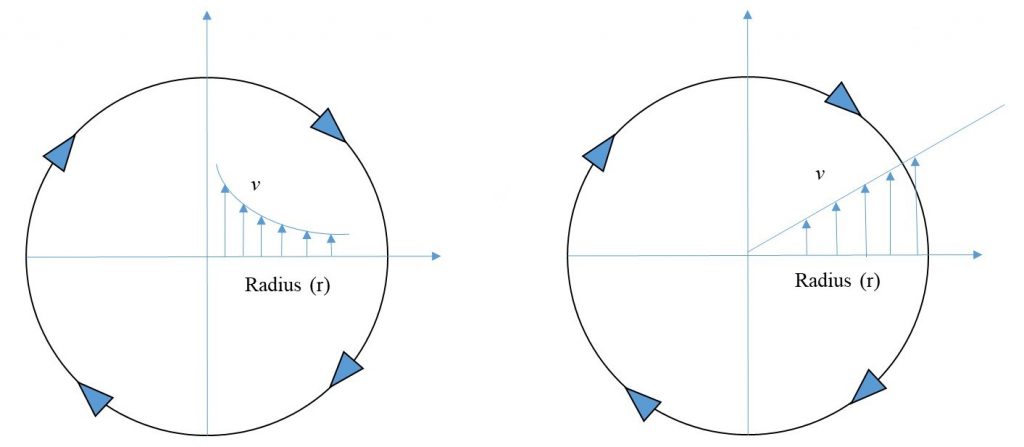
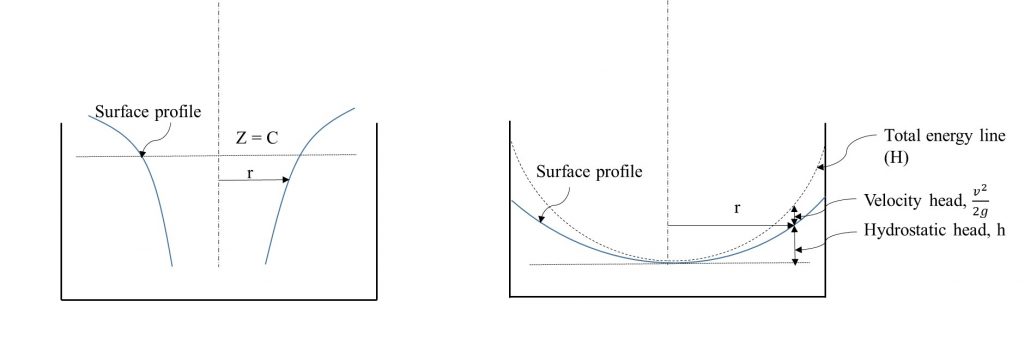
A free vortex is formed when water flows out of a vessel through a central hole in the base (Figure 8.2). The degree of the rotation depends on the initial disturbance. In a free cylindrical vortex, the velocity varies inversely with the distance from the axis of rotation (Figure 8.3).
The equation governing the surface profile is derived from the Bernoulli’s theorem:
Substituting Equation (1) into (2) will give a new expression:
or:
which is the equation of a hyperbolic curve of nature (Figure 8.4)
This curve is asymptotic to the axis of rotation and to the horizontal plane through z=c.
When water is forced to rotate at a constant speed () (Figure 8.2), the velocity will be also constant and equal to:
The velocity head (or kinetic energy) can be calculated as:
Substituting Equation (5) into (6) results in:
If the horizontal plane passing through the lowest point of the vortex is selected as datum, the total energy is equal to:
where ho is the pressure head at the datum. Substituting hc from Equation (7) into (8) gives:
At r=0: H=0, therefore, ho=0 , and :
This is the equation of the water surface profile, which is a parabola (Figure 8.4).

This experiment will be performed in two parts: free vortex and forced vortex.
Note: The vortex profile tends to wander, so the vortex diameter- measuring gauge arm should be positioned at 90° to the main arm. This allows a meaningful vortex diameter measurement to be made.
Note: If the water level fluctuates, raise the free end of the outlet tube above the grade line of the water in the vessel, and then lower it again into the bench tank. Doing this will ensure that water discharges at the same rate that it flows in, thereby helping to maintain the water level.
Please visit this link for accessing excel workbook for this experiment.
Use the following tables to record your measurements.
| D (mm) | 24-mm Orifice | 16-mm Orifice | 8-mm Orifice |
| H (mm) | |||
| 80 | |||
| 70 | |||
| 60 | |||
| 50 | |||
| 45 | |||
| 40 | |||
| 35 | |||
| 30 | |||
| No. of Revolutions (N) | T (sec) | Distance from center, r(mm) | ||||||
| 125 (edge) | 110 | 90 | 70 | 50 | 30 | 0 | ||
| Measured height, H(mm) | ||||||||
| 10 | ||||||||
| 20 | ||||||||
| 40 | ||||||||
| 50 | ||||||||
Record the coordinate points (D and H) for the three vortex profiles, using Figure 8.5 and the Raw Data Table – Free Vortex.
| 24-mm orifice | 16-mm orifice | 8-mm orifice | |||
| D (mm) | H (mm) | D (mm) | H (mm) | D (mm) | H (mm) |
| 80 | 80 | 80 | |||
| 70 | 70 | 70 | |||
| 60 | 60 | 60 | |||
| 50 | 50 | 50 | |||
| 45 | 45 | 45 | |||
| 40 | 40 | 40 | |||
| 35 | 35 | 35 | |||
| 30 | 30 | 30 | |||
For all series of experiments with N=10, 20, 40, and 50,
| Distance from the center, r (mm) | N=10 | N = 20 | N = 40 | N = 50 | ||||||||
| ω (rad/s) | H (mm) cal. | H (mm) meas. | ω (rad/s) | H (mm) cal. | H (mm) meas. | ω (rad/s) | H (mm) cal. | H (mm) meas. | ω (rad/s) | H (mm) cal. | H (mm) meas. | |
| 0 | ||||||||||||
| 30 | ||||||||||||
| 50 | ||||||||||||
| 70 | ||||||||||||
| 90 | ||||||||||||
| 110 | ||||||||||||
| 125 | ||||||||||||
cal.= calculated; meas.= measured.
Use the template provided to prepare your lab report for this experiment. Your report should include the following:
9
A weir is a barrier across the width of a river or stream that alters the characteristics of the flow and usually results in a change in the height of the water level. Several types of weirs are designed for application in natural channels and laboratory flumes. Weirs can be broad-crested, short-crested, or sharp-crested. Sharp-crested weirs, commonly referred to as notches, are manufactured from sharp-edged thin plates. The relationship between the flow rate and water depth above the weir can be derived by applying the Bernoulli’s equation and by making some assumptions with regard to head loss and pressure distribution of the flow passing over the weir. A coefficient of discharge needs to be determined experimentally for each weir to account for errors in estimating the flow rate that is due to these assumptions.
Weirs are commonly used to measure or regulate flow in rivers, streams, irrigation canals, etc. Installing a weir in an open channel system causes critical depth to form over the weir. Since there is a unique relationship between the critical depth and discharge, a weir can be designed as a flow-measuring device. Weirs are also built to raise the water level in a channel to divert the flow to irrigation systems that are located at higher elevations.
The objectives of this experiment are to:
a) determine the characteristics of flow over a rectangular and a triangular weir, and
b) determine the value of the discharge coefficient for both notches.
The coefficients of discharge are determined by measuring the height of the water surface above the notch base and the corresponding flow rate. The general features of the flow can be determined by direct observation.
The following equipment is required to perform the flow over weirs experiment:
The flow over the weir apparatus includes the following elements that are used in conjunction with the flow channel in the molded bench top of the hydraulics bench (Figure 9.1).

The depth of water above the base of a weir is related to the flow rate through it; therefore, the weir can be used as a flow measuring device. The relationships of flow over weirs can be obtained by applying the energy equation from a point well upstream of the weir to a point just above the weir crest. This approach requires a number of assumptions, and it yields the following results:
where:
Q : flow rate;
H : height above the weir base;
b : width of rectangular weir (R-notch);
: angle of triangular weir (V-notch);
Cd: discharge coefficient to account for the effects of simplifying assumptions in the theory, which has to be determined by experiment [9].

This experiment will be performed by taking the following steps:
Note: To measure the datum height of the base of the notch (ho), position the instrument carrier as shown in Figure 9.3. Then carefully lower the gauge until the point is just above the notch base, and lock the coarse adjustment screw. Then, using the fine adjustment, adjust the gauge until the point just touches the water surface and take a reading, being careful not to damage the notch.
Note: The surface of the water will fall as it approaches the weir. This is particularly noticeable at high flow rates by high heads. To obtain an accurate measurement of the undisturbed water level above the crest of the weir, it is necessary to place the measuring gauge at a distance of at least three times the head above the weir.
Note: To obtain a sufficiently accurate result, collect around 25 liters of water each time, or collect the water for at least 120 seconds.

Please visit this link for accessing excel workbook for this experiment.
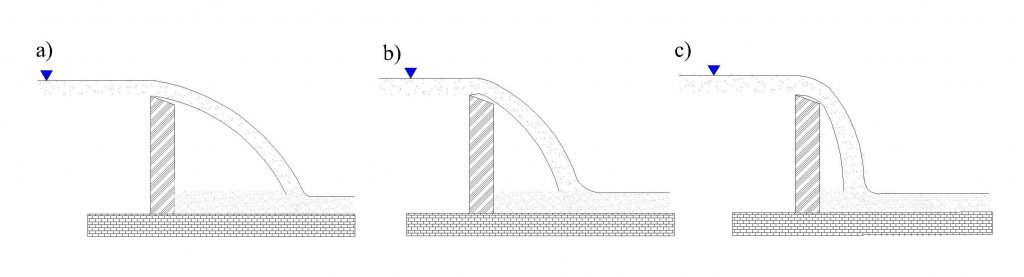
Use the following tables to record your measurements. Record any observations of the shape and the type of nappe, paying particular attention to whether the nappe was clinging or sprung clear, and of the end contraction and general change in shape. (See Figure 9.4 to classify the nappe).
| Test No. | Datum Height ho (m) | Water Surface Elev. h(m) | Volume Collected (L) | Time for Collection (s) |
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 6 | ||||
| 7 |
| Test No. | Datum Height ho (m) | Water Surface Elev. h(m) | Volume Collected (L) | Time for Collection (s) |
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 6 | ||||
| 7 |
The following dimensions from the equipment can be used in the appropriate calculations:
– width of rectangular notch (b) = 0.03 m
– angle of V-notch () = 90°
| No. | H (m) | Volume Collected (m3) | Flow Rate (m3/s) | H 3/2 | Experimental Cd | Theoretical Cd | %Error |
| 1 | |||||||
| 2 | |||||||
| 3 | |||||||
| 4 | |||||||
| 5 | |||||||
| 6 | |||||||
| 7 |
| No. | H (m) | Volume Collected (m3) | Flow Rate (m3/s) | H 3/2 | Experimental Cd | Theoretical Cd | %Error |
| 1 | |||||||
| 2 | |||||||
| 3 | |||||||
| 4 | |||||||
| 5 | |||||||
| 6 | |||||||
| 7 |
Use the template provided to prepare your lab report for this experiment. Your report should include the following:
10
In waterworks and wastewater systems, pumps are commonly installed at the source to raise the water level and at intermediate points to boost the water pressure. The components and design of a pumping station are vital to its effectiveness. Centrifugal pumps are most often used in water and wastewater systems, making it important to learn how they work and how to design them. Centrifugal pumps have several advantages over other types of pumps, including:
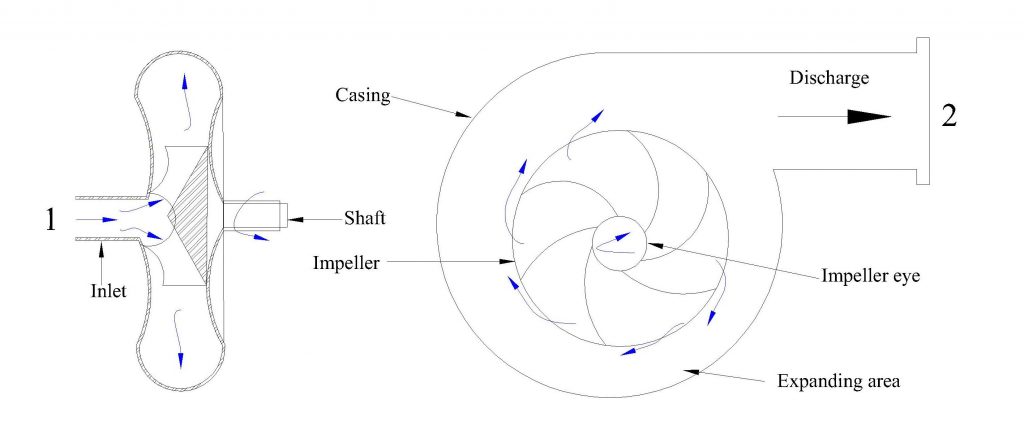
A centrifugal pump consists of a rotating shaft that is connected to an impeller, which is usually comprised of curved blades. The impeller rotates within its casing and sucks the fluid through the eye of the casing (point 1 in Figure 10.1). The fluid’s kinetic energy increases due to the energy added by the impeller and enters the discharge end of the casing that has an expanding area (point 2 in Figure 10.1). The pressure within the fluid increases accordingly.
The performance of a centrifugal pump is presented as characteristic curves in Figure 10.2, and is comprised of the following:
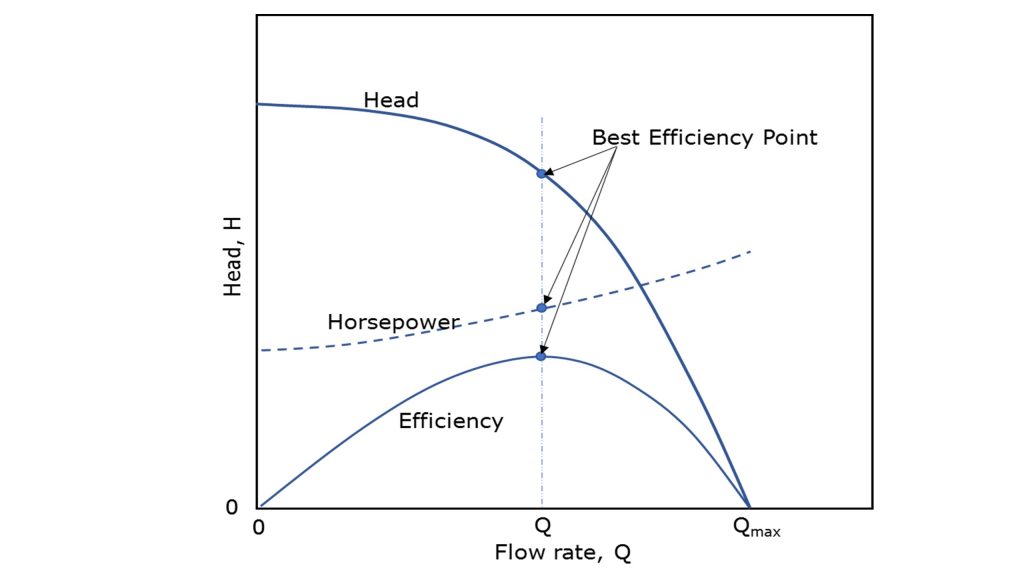
The characteristic curves of commercial pumps are provided by manufacturers. Otherwise, a pump should be tested in the laboratory, under various discharge and head conditions, to produce such curves. If a single pump is incapable of delivering the design flow rate and pressure, additional pumps, in series or parallel with the original pump, can be considered. The characteristic curves of pumps in series or parallel should be constructed since this information helps engineers select the types of pumps needed and how they should be configured.
Many pumps are in use around the world to handle liquids, gases, or liquid-solid mixtures. There are pumps in cars, swimming pools, boats, water treatment facilities, water wells, etc. Centrifugal pumps are commonly used in water, sewage, petroleum, and petrochemical pumping. It is important to select the pump that will best serve the project’s needs.
The objective of this experiment is to determine the operational characteristics of two centrifugal pumps when they are configured as a single pump, two pumps in series, and two pumps in parallel.
Each configuration (single pump, two pumps in series, and two pumps in parallel) will be tested at pump speeds of 60, 70, and 80 rev/sec. For each speed, the bench regulating valve will be set to fully closed, 25%, 50%, 75%, and 100% open. Timed water collections will be performed to determine flow rates for each test, and the head, hydraulic power, and overall efficiency ratings will be obtained.
The following equipment is required to perform the pumps experiment:
The hydraulics bench is fitted with a single centrifugal pump that is driven by a single-phase A.C. motor and controlled by a speed control unit. An auxiliary pump and the speed control unit are supplied to enhance the output of the bench so that experiments can be conducted with the pumps connected either in series or in parallel. Pressure gauges are installed at the inlet and outlet of the pumps to measure the pressure head before and after each pump. A watt-meter unit is used to measure the pumps’ input electrical power [10].
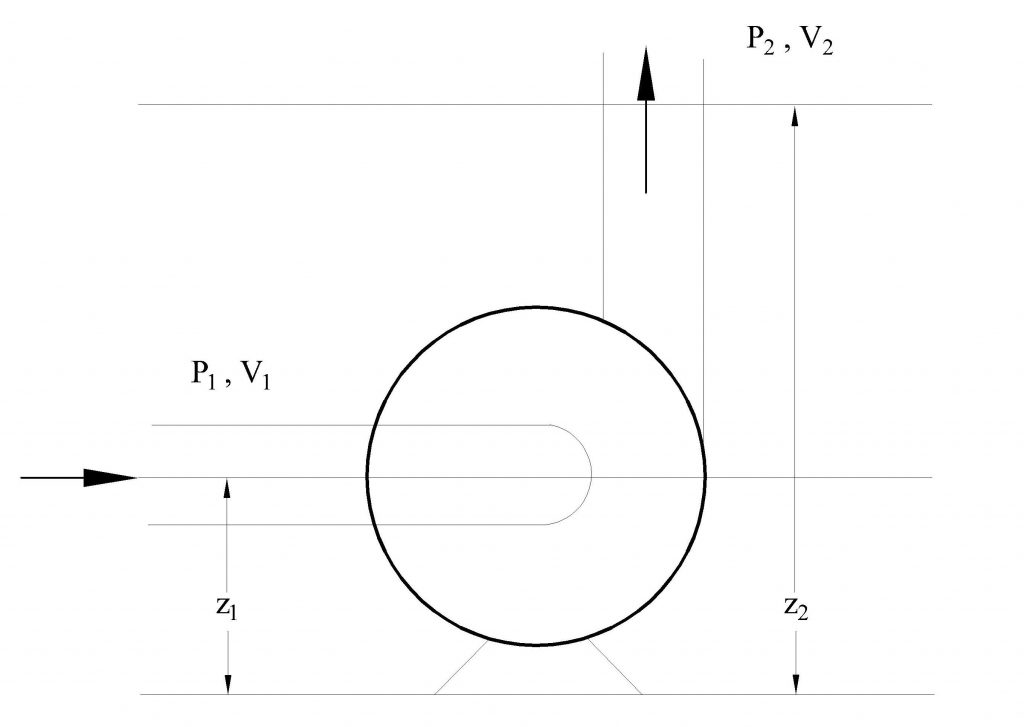
Consider the pump shown in Figure 10.3. The work done by the pump, per unit mass of fluid, will result in increases in the pressure head, velocity head, and potential head of the fluid between points 1 and 2. Therefore:
in which:
W: work
M: mass
P: pressure
: density
v: flow velocity
g: acceleration due to gravity
z: elevation
Applying Bernoulli’s equation between points 1 and 2 in Figure 10.3 results in:
Since the difference between elevations and velocities at points 1 and 2 are negligible, the equation becomes:
Dividing both sides of this equation by gives:
The right side of this equation is the manometric pressure head, Hm, therefore:
The hydraulic power (Wh) supplied to the fluid by the pump is the product of the pressure increase and the flow rate:
The pressure increase produced by the pump can be expressed in terms of the manometric head,
Therefore:
The overall efficiency () of the pump-motor unit can be determined by dividing the hydraulic power (Wh) by the input electrical power (Wi), i.e.:
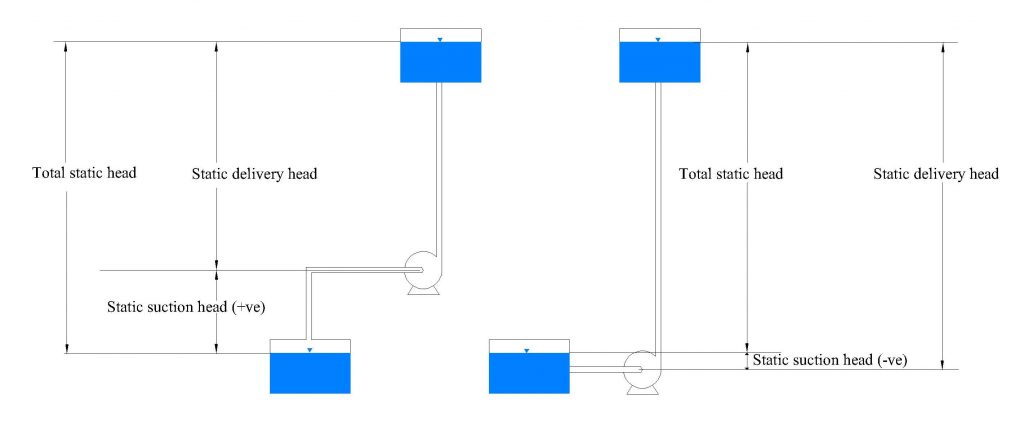
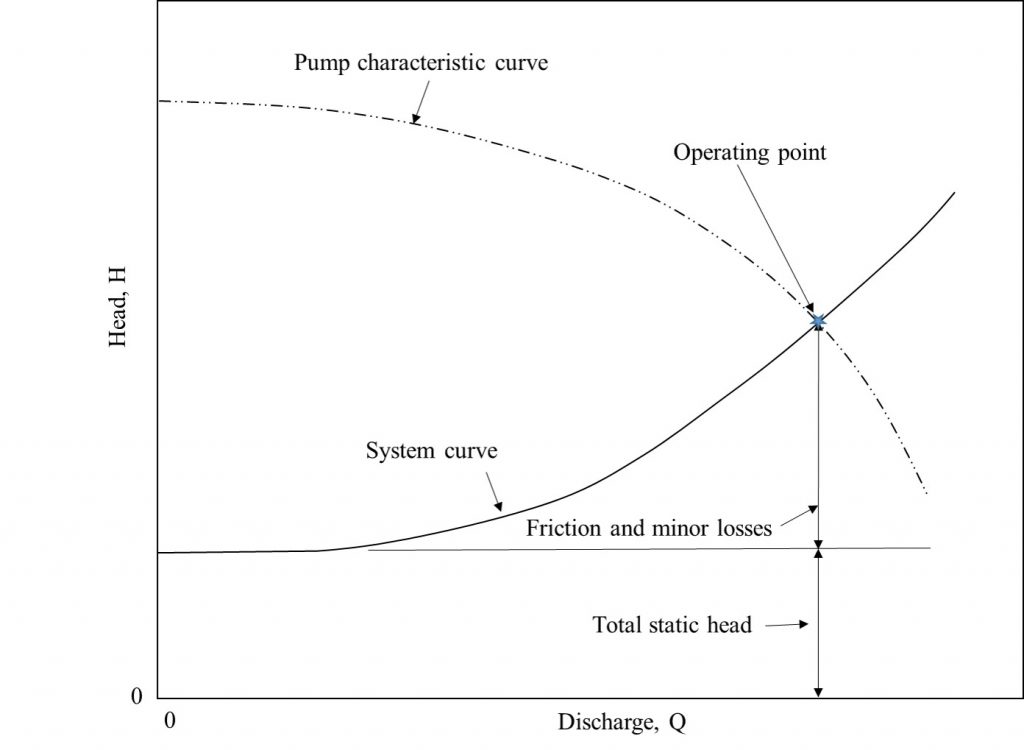
While pumping fluid, the pump has to overcome the pressure loss that is caused by friction in any valves, pipes, and fittings in the pipe system. This frictional head loss is approximately proportional to the square of the flow rate. The total system head that the pump has to overcome is the sum of the total static head and the frictional head. The total static head is the sum of the static suction lift and the static discharge head, which is equal to the difference between the water levels of the discharge and the source tank (Figure 10.4). A plot of the total head-discharge for a pipe system is called a system curve; it is superimposed onto a pump characteristic curve in Figure 10.5. The operating point for the pump-pipe system combination occurs where the two graphs intercept [10].
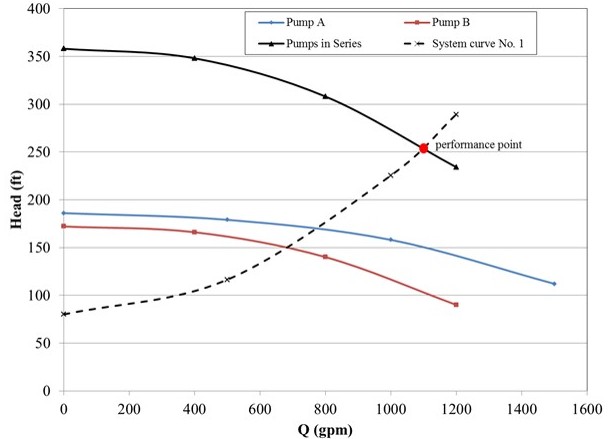
Pumps are used in series in a system where substantial head changes take place without any appreciable difference in discharge. When two or more pumps are configured in series, the flow rate throughout the pumps remains the same; however, each pump contributes to the increase in the head so that the overall head is equal to the sum of the contributions of each pump [10]. For n pumps in series:
The composite characteristic curve of pumps in series can be prepared by adding the ordinates (heads) of all of the pumps for the same values of discharge. The intersection point of the composite head characteristic curve and the system curve provides the operating conditions (performance point) of the pumps (Figure 10.6).
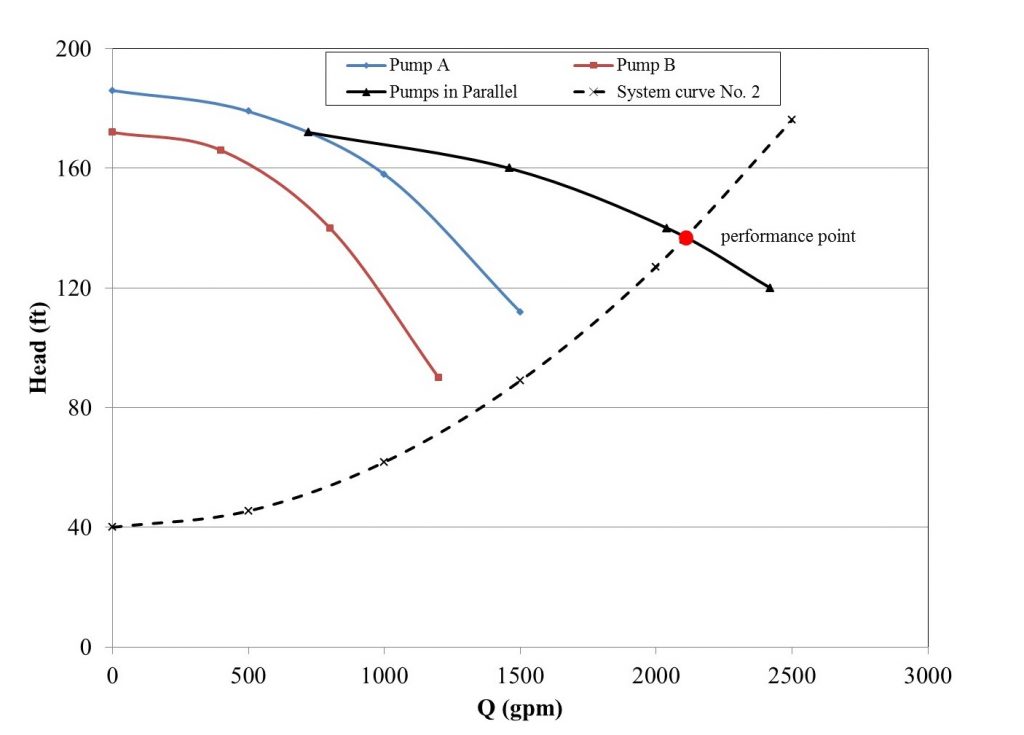
Parallel pumps are useful for systems with considerable discharge variations and with no appreciable head change. In parallel, each pump has the same head. However, each pump contributes to the discharge so that the total discharge is equal to the sum of the contributions of each pump [10]. Thus for pumps:
The composite head characteristic curve is obtained by summing up the discharge of all pumps for the same values of head. A typical pipe system curve and performance point of the pumps are shown in Figure 10.7.
a) Set up the hydraulics bench valves, as shown in Figure 10.8, to perform the single pump test.
b) Start pump 1, and increase the speed until the pump is operating at 60 rev/sec.
c) Turn the bench regulating valve to the fully closed position.
d) Record the pump 1 inlet pressure (P1) and outlet pressure (P2). Record the input power from the watt-meter (Wi). (With the regulating valve fully closed, discharge will be zero.)
e) Repeat steps (c) and (d) by setting the bench regulating valve to 25%, 50%, 75%, and 100% open.
f) For each control valve position, measure the flow rate by either collecting a suitable volume of water (a minimum of 10 liters) in the measuring tank, or by using the rotameter.
g) Increase the speed until the pump is operating at 70 rev/sec and 80 rev/sec, and repeat steps (c) to (f) for each speed.
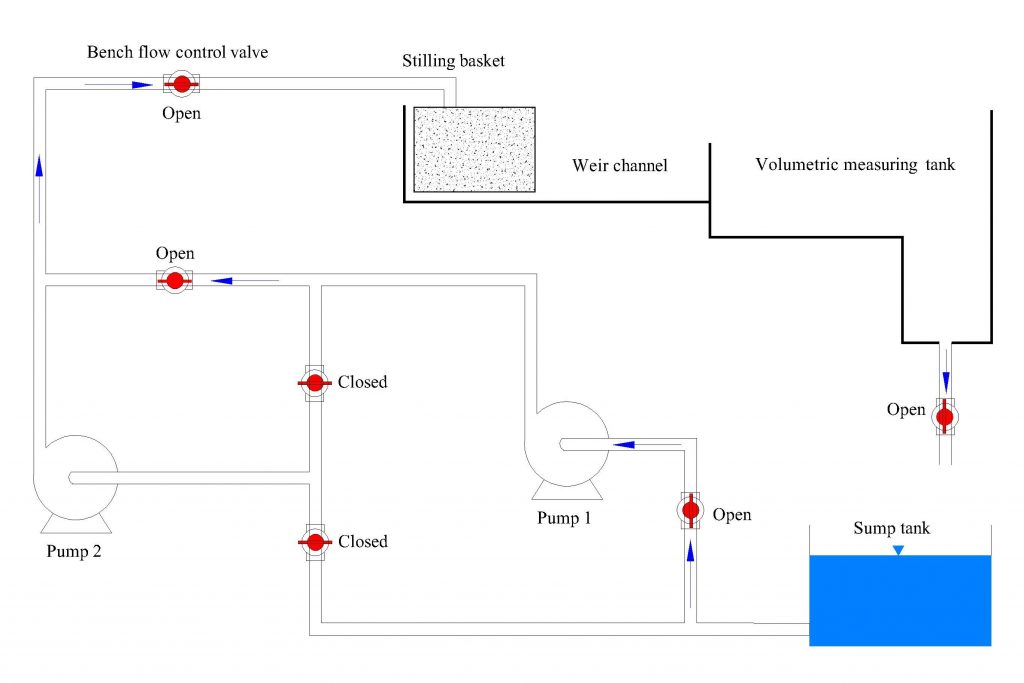
a) Set up the hydraulics bench valves, as shown in Figure 10.9, to perform the two pumps in series test.
b) Start pumps 1 and 2, and increase the speed until the pumps are operating at 60 rev/sec.
c) Turn the bench regulating valve to the fully closed position.
d) Record the pump 1 and 2 inlet pressure (P1) and outlet pressure (P2). Record the input power for pump 1 from the wattmeter (Wi). (With the regulating valve fully closed, discharge will be zero.)
e) Repeat steps (c) and (d) by setting the bench regulating valve to 25%, 50%, 75%, and 100% open.
f) For each control valve position, measure the flow rate by either collecting a suitable volume of water (a minimum of 10 liters) in the measuring tank, or by using the rotameter.
g) Increase the speed until the pump is operating at 70 rev/sec and 80 rev/sec, and repeat steps (c) to (f) for each speed.
Note: Wattmeter readings should be recorded for both pumps, assuming that both pumps have the same input power.
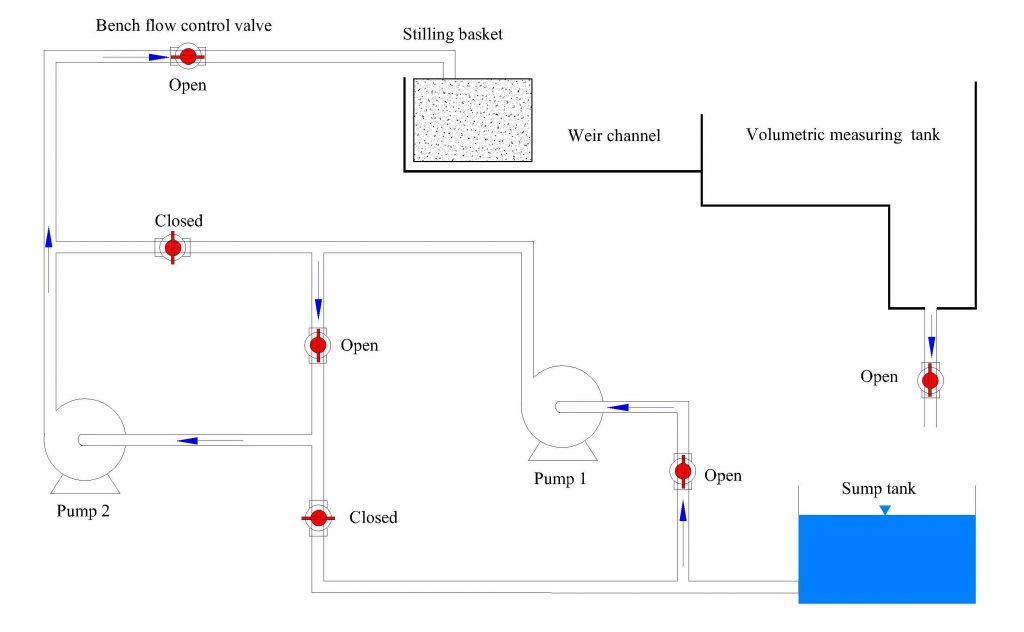
a) Configure the hydraulic bench, as shown in Figure 10.10, to conduct the test for pumps in parallel.
b) Repeat steps (b) to (g) in Experiment 2.
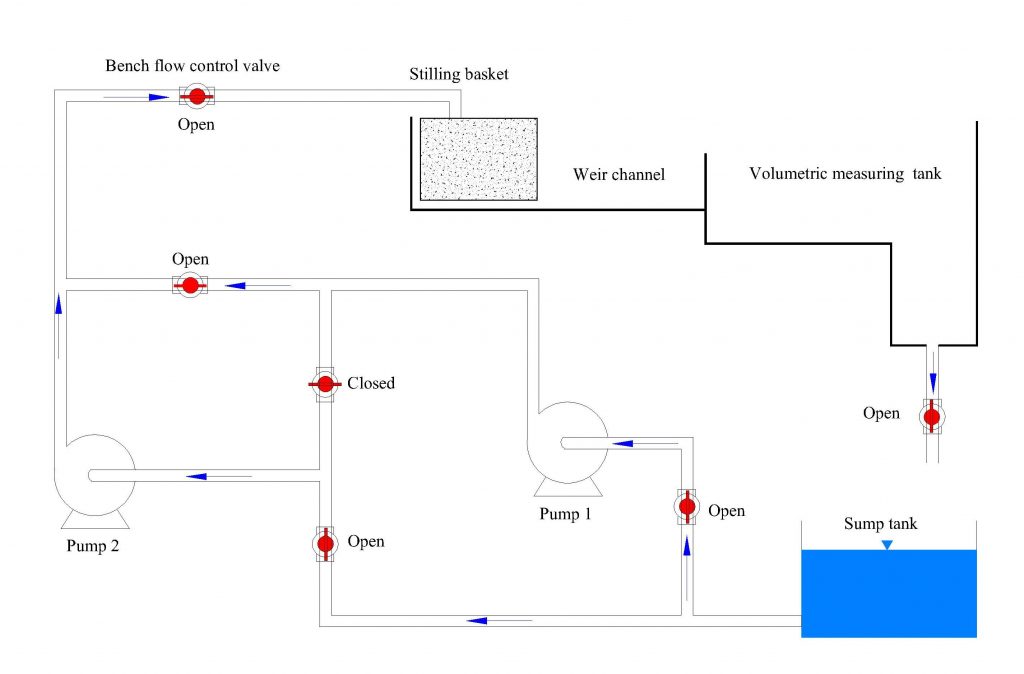
Please visit this link for accessing excel workbook of this manual.
Record your measurements for Experiments 1 to 3 in the Raw Data Tables.
| Single Pump: 60 rev/s | |||||
| Valve Open Position | 0% | 25% | 50% | 75% | 100% |
| Volume (L) | |||||
| Time (s) | |||||
| Pump 1 Inlet Pressure, P1 (bar) | |||||
| Pump 1 Outlet Pressure, P2 (bar) | |||||
| Pump 1 Electrical Input Power (Wi) | |||||
| Single Pump: 70 rev/s | |||||
| Valve Open Position | 0% | 25% | 50% | 75% | 100% |
| Volume (L) | |||||
| Time (s) | |||||
| Pump 1 Inlet Pressure, P1 (bar) | |||||
| Pump 1 Outlet Pressure, P2 (bar) | |||||
| Pump 1 Electrical Input Power (Wi) | |||||
| Single Pump: 80 rev/s | |||||
| Valve Open Position | 0% | 25% | 50% | 75% | 100% |
| Volume (L) | |||||
| Time (s) | |||||
| Pump 1 Inlet Pressure, P1 (bar) | |||||
| Pump 1 Outlet Pressure, P2 (bar) | |||||
| Pump 1 Electrical Input Power (Wi) | |||||
| Two Pumps in Series: 60 rev/s | |||||
| Valve Open Position | 0% | 25% | 50% | 75% | 100% |
| Volume (L) | |||||
| Time (s) | |||||
| Pump 1 Inlet Pressure, P1 (bar) | |||||
| Pump 1 Outlet Pressure, P2 (bar) | |||||
| Pump 1 Electrical Input Power (Wi) | |||||
| Pump 2 Inlet Pressure, P1 (bar) | |||||
| Pump 2 Outlet Pressure, P2 (bar) | |||||
| Pump 2 Electrical Input Power (Wi) | |||||
| Two Pumps in Series: 70 rev/s | |||||
| Valve Open Position | 0% | 25% | 50% | 75% | 100% |
| Volume (L) | |||||
| Time (s) | |||||
| Pump 1 Inlet Pressure, P1 (bar) | |||||
| Pump 1 Outlet Pressure, P2 (bar) | |||||
| Pump 1 Electrical Input Power (Wi) | |||||
| Pump 2 Inlet Pressure, P1 (bar) | |||||
| Pump 2 Outlet Pressure, P2 (bar) | |||||
| Pump 2 Electrical Input Power (Wi) | |||||
| Two Pumps in Series: 80 rev/s | |||||
| Valve Open Position | 0% | 25% | 50% | 75% | 100% |
| Volume (L) | |||||
| Time (s) | |||||
| Pump 1 Inlet Pressure, P1 (bar) | |||||
| Pump 1 Outlet Pressure, P2 (bar) | |||||
| Pump 1 Electrical Input Power (Wi) | |||||
| Pump 2 Inlet Pressure, P1 (bar) | |||||
| Pump 2 Outlet Pressure, P2 (bar) | |||||
| Pump 2 Electrical Input Power (Wi) | |||||
| Two Pumps in Parallel: 60 rev/s | |||||
| Valve Open Position | 0% | 25% | 50% | 75% | 100% |
| Volume (L) | |||||
| Time (s) | |||||
| Pump 1 Inlet Pressure, P1 (bar) | |||||
| Pump 1 Outlet Pressure, P2 (bar) | |||||
| Pump 1 Electrical Input Power (Wi) | |||||
| Pump 2 Inlet Pressure, P1 (bar) | |||||
| Pump 2 Outlet Pressure, P2 (bar) | |||||
| Pump 2 Electrical Input Power (Wi) | |||||
| Two Pumps in Parallel: 70 rev/s | |||||
| Valve Open Position | 0% | 25% | 50% | 75% | 100% |
| Volume (L) | |||||
| Time (s) | |||||
| Pump 1 Inlet Pressure, P1 (bar) | |||||
| Pump 1 Outlet Pressure, P2 (bar) | |||||
| Pump 1 Electrical Input Power (Wi) | |||||
| Pump 2 Inlet Pressure, P1 (bar) | |||||
| Pump 2 Outlet Pressure, P2 (bar) | |||||
| Pump 2 Electrical Input Power (Wi) | |||||
| Two Pumps in Parallel: 80 rev/s | |||||
| Valve Open Position | 0% | 25% | 50% | 75% | 100% |
| Volume (L) | |||||
| Time (s) | |||||
| Pump 1 Inlet Pressure, P1 (bar) | |||||
| Pump 1 Outlet Pressure, P2 (bar) | |||||
| Pump 1 Electrical Input Power (Wi) | |||||
| Pump 2 Inlet Pressure, P1 (bar) | |||||
| Pump 2 Outlet Pressure, P2 (bar) | |||||
| Pump 2 Electrical Input Power (Wi) | |||||
Note:
– Overall head for pumps in series is calculated using Equation 8b.
– Overall head for pumps in parallel is calculated using Equation 9b.
– Overall electrical input power for pumps in series and in parallel combination is equal to (Wi)pump1+(Wi)pump2.
| Single Pump: N (rev/s) | |||||
| Valve Open Position | 0% | 25% | 50% | 75% | 100% |
| Flow Rate, Q (L/min) | |||||
| Flow Rate, Q (m3/s) | |||||
| Pump 1 Inlet Pressure, P1 (N/m2) | |||||
| Pump 1 Outlet Corrected Pressure, P2 (N/m2) | |||||
| Pump 1 Electrical Input Power (Watts) | |||||
| Pump 1 Head, Hm (m) | |||||
| Pump 1 Hydraulic Power, Wh (Watts) | |||||
| Pump 1 Overall Efficiency, η0 (%) | |||||
| Two Pumps in Series: N (rev/s) | |||||
| Valve Open Position | 0% | 25% | 50% | 75% | 100% |
| Flow Rate, Q (L/min) | |||||
| Flow Rate, Q (m3/s) | |||||
| Pump 1 Inlet Pressure, P1 (N/m2) | |||||
| Pump 1 Outlet Corrected Pressure, P2 (N/m2) | |||||
| Pump 1 Electrical Input Power (Watts) | |||||
| Pump 2 Inlet Pressure, P1 (N/m2) | |||||
| Pump 2 Outlet Corrected Pressure, P2 (N/m2) | |||||
| Pump 2 Electrical Input Power (Watts) | |||||
| Pump 1 Head, Hm (m) | |||||
| Pump 1 Hydraulic Power, Wh (Watts) | |||||
| Pump 2 Head, Hm (m) | |||||
| Pump 2 Hydraulic Power, Wh (Watts) | |||||
| Overall Head, Hm (m) | |||||
| Overall Hydraulic Power, Wh (Watts) | |||||
| Overall Electrical Input Power, Wi (Watts) | |||||
| Both Pumps Overall Efficiency, η0 (%) | |||||
| Two Pumps in Parallel: N (rev/s) | |||||
| Valve Open Position | 0% | 25% | 50% | 75% | 100% |
| Flow Rate, Q (L/min) | |||||
| Flow Rate, Q (m3/s) | |||||
| Pump 1 Inlet Pressure, P1 (N/m2) | |||||
| Pump 1 Outlet Corrected Pressure, P2 (N/m2) | |||||
| Pump 1 Electrical Input Power (Watts) | |||||
| Pump 2 Inlet Pressure, P1 (N/m2) | |||||
| Pump 2 Outlet Corrected Pressure, P2 (N/m2) | |||||
| Pump 2 Electrical Input Power (Watts) | |||||
| Pump 1 Head, Hm (m) | |||||
| Pump 1 Hydraulic Power, Wh (Watts) | |||||
| Pump 2 Head, Hm (m) | |||||
| Pump 2 Hydraulic Power, Wh (Watts) | |||||
| Overall Head, Hm (m) | |||||
| Overall Hydraulic Power, Wh (Watts) | |||||
| Overall Electrical Input Power, Wi (Watts) | |||||
| Both Pumps Overall Efficiency, η0 (%) | |||||
Use the template provided to prepare your lab report for this experiment. Your report should include the following:
In each of above graphs, show the results for single pump, two pumps in series, and two pumps in parallel – a total of three graphs. Do not connect the experimental data points, and use best fit to plot the graphs
1
2
Introduction Video (https://bit.ly/2stFm3p)
Experiment #1: Hydrostatic Pressure (https://bit.ly/2RHk9x9)
Experiment #2: Bernoulli’s Theorem Demonstration (https://bit.ly/2PbQ9rU)
Experiment #3: Energy Loss in Pipe Fittings (https://bit.ly/2t0PvEM)
Experiment #4: Energy Loss in Pipes (https://bit.ly/2LIxTUO)
Experiment #5: Impact of a Jet (https://bit.ly/2ryb13r)
Experiment #6: Orifice and Free Jet Flow (https://bit.ly/357Coju)
Experiment #7: Osborne Reynolds’ Demonstration (https://bit.ly/35aMXSS)
Experiment #8: Free and Forced Vortices (https://bit.ly/2LHZaa2)
Experiment #9: Flow Over Weirs (https://bit.ly/2YzowvI)
Experiment #10: Pumps (http://bit.ly/2PVO42a)
Experiment #1: Hydrostatic Pressure (https://youtu.be/LfqadPBKim8)
Experiment #2: Bernoulli’s Theorem Demonstration (https://youtu.be/Qlie8g_YYPc)
Experiment #3: Energy Loss in Pipe Fittings (https://youtu.be/LvbUN79Arlc)
Experiment #4: Energy Loss in Pipes (https://youtu.be/CuuNFqIEhQg)
Experiment #5: Impact of a Jet (https://youtu.be/ndjMiwWA4CI)
Experiment #6: Orifice and Free Jet Flow (https://youtu.be/x3bVnho3NXc)
Experiment #7: Osborne Reynolds’ Demonstration (https://youtu.be/7MpO8kuJvzE)
Experiment #8: Free and Forced Vortices (https://youtu.be/YKTh9CO-5c0)
Experiment #9: Flow Over Weirs (https://youtu.be/cNuI0SCWN0M)
Experiment #10: Pumps (https://youtu.be/qI-pMiu3xug)
3
This work contains copyrighted material the use of which has not always been specifically authorized by the copyright owners. The creators of this OER believe in good faith that reuse of these materials constitutes a “fair use” as described in Section 107 of the Copyright Act. Downstream users who wish to use copyrighted material from this resource for purposes beyond those authorized by the fair use doctrine should obtain permission from the copyright owner(s) of the original content.
Unless noted below, all figures used in the text are the intellectual property of the content creators and are licensed under a Creative Commons Attribution 4.0 International license.
Figure 4.1: “Moody diagram. Lines created using Swami and Jaine formula.” Plot created on Matlab. By S Beck and R Collins, University of Sheffield, 2008. Wiki Commons. (https://commons.wikimedia.org/wiki/File:Moody_diagram.jpg)