Introduction
The triaxial shear test is the most versatile of all of the methods for testing the shear strength of soil and finding its cohesion (c) and angle of internal friction (φ). It can measure the total, as well as the effective stress parameters, and can be conducted on any type of soil. Drainage conditions can be controlled, and pore water pressure and volume changes can be measured accurately. The failure plane is not forced in this test, and the stress distribution of the failure plane is fairly uniform. Specimens can fail on any weak plane or can simply bulge.
The three primary triaxial tests conducted in the laboratory each allow the soil response for differing engineering applications to be observed. These are:
- Unconsolidated undrained test (UU)
- Consolidated undrained test (CU)
- Consolidated drained test (CD)
The unconsolidated undrained (UU) test is the simplest and fastest. The soil specimens are loaded, and only the total stresses are controlled and recorded. This allows determination of the undrained shear strength, cu, which is suitable for assessing the soil stability in the short-term (e.g., during or directly following a construction project). The test is generally performed on cohesive soil specimens; however, remolded sand samples can also be tested. The consolidated drained (CD) test describes the long-term loading response, and provides the strength parameters determined under effective stress control (i.e. φ and c’). It can take a significant time to complete when using cohesive soil, because the shear rate must be slow enough to allow negligible pore water pressure changes. Finally, the consolidated undrained (CU) test is the most common triaxial procedure, as it allows strength parameters to be determined based on the effective stresses (i.e., φ’ and c’) while permitting a faster rate of shearing than the CD test. This is achieved by recording the excess pore pressure change that occurs within the specimen as shearing takes place. In this manual, the basics of the UU triaxial test is covered.
Practical Application
The triaxial test, which determines the shear strength and stiffness of soil and rock, is one of the most versatile and widely performed geotechnical laboratory tests that is used in geotechnical design.
Two parameters of shear strength are required for the design of slopes and for many other analyses: calculation of the bearing capacity of any strata, and calculation of the consolidation parameters.
Objective
The objective of this experiment is
- To determine the soil strength parameters
Equipment
- Triaxial test setup
- Sample tubes
- Rubber ring
- Open ended cylindrical section
- Weighing balance
Standard Reference
- ASTM D4767: Standard Test Method for Consolidated Undrained Triaxial Compression Test for Cohesive Soils
Method
The general triaxial test procedure is discussed below.
Specimen & System Preparation
After a test specimen has been prepared from a soil sample, it is placed it into the triaxial cell. For cohesive soils, this may involve trimming undisturbed specimens extruded from Shelby tubes or cut from block samples. Granular soil specimens may require preparation directly on the pedestal, using a split-part mold. A membrane suction stretcher can be used to place the rubber membrane around the soil specimen once it is in position on the pedestal. Note that disturbance to the specimen should be kept to a minimum during the specimen preparation.
The triaxial cell other system components are assembled after placement of the specimen. During this stage, the cell is filled with fluid, the pressure/volume controllers are connected, and transducer readings are set.
Saturation
The saturation process is designed to ensure that all voids within the test specimen are filled with water, and that the pore pressure transducer and drainage lines are properly de-aired. This may be achieved by applying a partial vacuum to the specimen to remove air and draw water into the transducer and drainage lines, followed by a linear increase of the cell and back pressures. At no point should the effective stress increase above the value required for shearing, as this leads to specimen over-consolidation. To assist the specimen in reaching full saturation, the following steps may be taken:
- Use de-aired water to fill voids in the specimens.
- Increase the back pressure to force air into the solution.
Before moving to the consolidation stage, a short test is performed to determine Skempton’s B value to see whether the specimen’s degree saturation is sufficiently high. This is called a B-check and requires that the specimen drainage is closed while the cell pressure is raised by approximately 50 kPa. Note, however, that B is soil-dependent, so while a normally consolidated soft clay will produce B ≈ 1.00 at full saturation, a very dense sand or stiff clay may only show B ≈ 0.91, even if full saturation has been reached.
Consolidation
The consolidation stage is used to bring the specimen to the effective stress state required for shearing. It is typically conducted by increasing the cell pressure while maintaining a constant back pressure that is often equal to the pore pressure reached during the final saturation B-check. This process is continued until the volume change (ΔV) of the specimen is no longer significant and at least 95% of the excess pore pressure has dissipated. The consolidation response can also be used to estimate a suitable rate of strain when shearing cohesive specimens.
Shearing
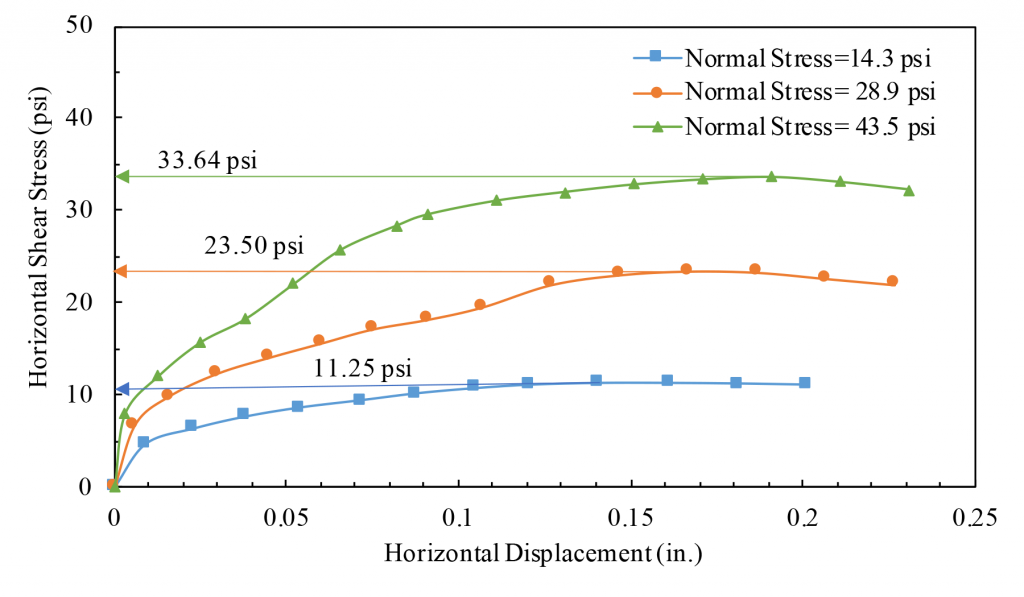
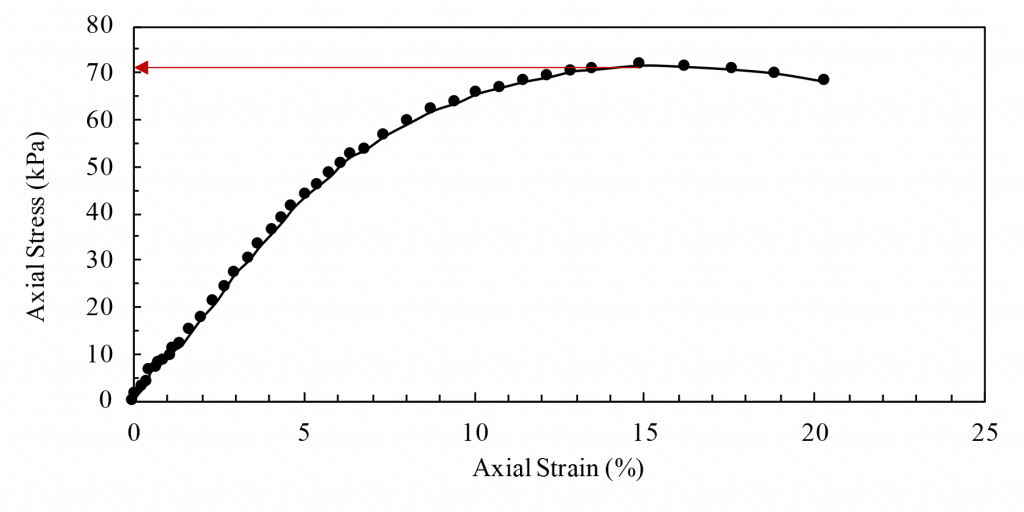
The soil is sheared by applying an axial strain, εa, to the test specimen at a constant rate through upward (compression) or downward (extension) movement of the load frame platen. This rate, along with the specimen drainage condition, is dependent on the type of triaxial test being performed. Specimen response during the shear stage is typically monitored by plotting the deviator stress q or effective principal stress ratio (σ1/σ3) against the axial strain, εa. This stage is continued until a specified failure criterion has been reached, which may include identifying the peak deviator stress or peak effective principal stress ratio; observing the constant stress and excess pore pressure/volume change values; or simply reaching a specific value of axial strain.

Figure 10.1: Measuring the specimen

Figure 10.2: Triaxial test apparatus

Figure 10.3: Placing the specimen on the triaxial base

Figure 10.4: Setting up the apparatus

Figure 10.5: Triaxial control panel

Figure 10.6: Triaxial loading base
Video Materials
Lecture Video
A PowerPoint presentation is created to understand the background and method of this experiment.
Demonstration Video
A short video is executed to demonstrate the experiment procedure and sample calculation.
Results and Discussions
A sample calculation is shown for the unconsolidated undrained triaxial test.
Calculate Axial Strain:
ε= ΔL/ L
Where,
ΔL = change in length of specimen as read from deformation indicator, mm (in.)
L0 = initial length of specimen minus any change in length prior to loading, mm (in.)
Calculate the average cross-sectional area for a given applied axial load (Ap):
Ap= Ao/(1-ε)
Determine the principal stresses at failure:
Minor principal stress (3):
σ3= Chamber pressure
Major principle stress (1):
σ1= Deviator stress at failure plus chamber pressure
Calculate the deviator stress for a given applied load: (σ1 – σ3)= P/Ap
Where,
Ap = initial average cross-sectional area of the specimen, m2(in.2)
P = given applied axial load (corrected for uplift and piston friction, if required), kPa (psi).
Graph the relationship between deviator stress (principal stress difference) and axial strain, plotting the deviator stress as ordinate and axial strain as abscissa. When testing a large number of samples, failure occurs when the same stresses are obtained for three or more consecutive strain readings. Graph the circle of stress as shown in Figure 10.7.
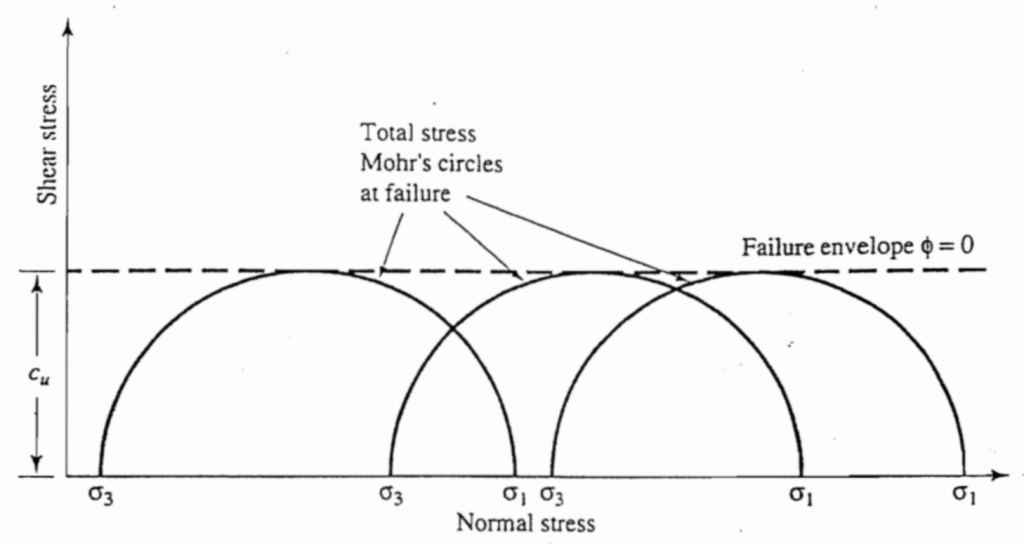
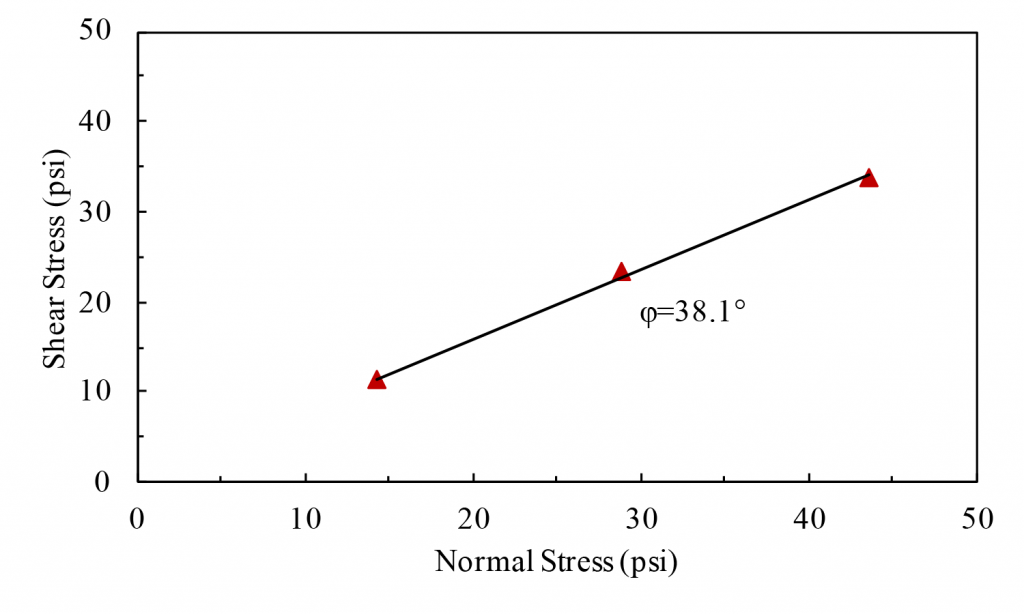
Figure 10.7: Total stress Mohr’s circles and failure envelope(φ=0)obtained from unconsolidated undrained triaxial tests on fully saturated cohesive soil
Report
Use the template provided to prepare your lab report for this experiment. Your report should include the following:
- Objective of the test
- Applications of the test
- Apparatus used
- Test procedures (optional)
- Analysis of test results – Complete the table provided and show one sample calculation.
- Summary and conclusions – Comment on the shear strength value of the soil.

 Dr. Sahadat Hossain is a Professor of Civil Engineering Department and Director of Solid Waste Institute for Sustainability (SWIS) at the University of Texas at Arlington. Dr. Hossain has more than 25 (twenty-five) years of professional and research experience in geotechnical and geo-environmental engineering. Dr. Hossain’s research experience includes slope stability analysis, innovative slope stabilization techniques, assessment of geo-hazard potential, and recycled aggregate materials for base and sub-base applications, pavement crack mitigation, and sustainable waste management. One of his most recent successfully implemented projects is slope stabilization with Recycled Plastic Pins (RPP), which is a major signature project in Texas. He also worked on more than 150 (One Hundred and Fifty) geotechnical design and construction projects in Bangladesh, Singapore, Hong Kong, Malaysia, Thailand and USA as a Civil/Geotechnical engineer. His working experiences include foundation analysis and design for building and bridge, excavation support system and retaining structures, cut and cover tunneling, slope stability analysis, design and construction of drilled shaft, contiguous bored pile wall, secant pile wall and diaphragm wall. Dr. Hossain has coauthored two books titled “Sustainable Slope Stabilization using Recycled Plastic Pins” and “Site Investigations by Resistivity Imaging” published by CRC press. Dr. Hossain received his bachelor’s degree from Indian Institute of Technology (IIT), Bombay, India in 1994 and master’s degree in Geotechnical Engineering from Asian Institute of Technology (AIT), Bangkok, Thailand in 1997. He received his PhD degree in Geo-Environmental Engineering from North Carolina State University (NCSU) at Raleigh, USA in 2002.
Dr. Sahadat Hossain is a Professor of Civil Engineering Department and Director of Solid Waste Institute for Sustainability (SWIS) at the University of Texas at Arlington. Dr. Hossain has more than 25 (twenty-five) years of professional and research experience in geotechnical and geo-environmental engineering. Dr. Hossain’s research experience includes slope stability analysis, innovative slope stabilization techniques, assessment of geo-hazard potential, and recycled aggregate materials for base and sub-base applications, pavement crack mitigation, and sustainable waste management. One of his most recent successfully implemented projects is slope stabilization with Recycled Plastic Pins (RPP), which is a major signature project in Texas. He also worked on more than 150 (One Hundred and Fifty) geotechnical design and construction projects in Bangladesh, Singapore, Hong Kong, Malaysia, Thailand and USA as a Civil/Geotechnical engineer. His working experiences include foundation analysis and design for building and bridge, excavation support system and retaining structures, cut and cover tunneling, slope stability analysis, design and construction of drilled shaft, contiguous bored pile wall, secant pile wall and diaphragm wall. Dr. Hossain has coauthored two books titled “Sustainable Slope Stabilization using Recycled Plastic Pins” and “Site Investigations by Resistivity Imaging” published by CRC press. Dr. Hossain received his bachelor’s degree from Indian Institute of Technology (IIT), Bombay, India in 1994 and master’s degree in Geotechnical Engineering from Asian Institute of Technology (AIT), Bangkok, Thailand in 1997. He received his PhD degree in Geo-Environmental Engineering from North Carolina State University (NCSU) at Raleigh, USA in 2002. Mr. Md Azijul Islam is a Ph.D. candidate at the University of Texas at Arlington. He completed his B.Sc. and M.Sc. in Civil Engineering from Bangladesh University of Engineering and Technology (BUET). He worked as a lecturer and later as an assistant professor at the Department of Civil Engineering, BUET from 2015 to 2018. Mr. Azijul has more than 5 (five) years of professional, teaching and research experience in geotechnical and geo-environmental engineering. His research interests include ground improvement, foundation engineering, pavement materials, slope stability analysis and landslide prevention, and disaster management. Mr. Azijul has published in journals and conference proceedings. He has been serving as a reviewer in reputed international journals. He was awarded “Outstanding Civil Engineering Ph.D. Student” in recognition of academic excellence in Civil Engineering in 2018-19 and 2019-20 session. He wants to pursue his career in research and teaching profession.
Mr. Md Azijul Islam is a Ph.D. candidate at the University of Texas at Arlington. He completed his B.Sc. and M.Sc. in Civil Engineering from Bangladesh University of Engineering and Technology (BUET). He worked as a lecturer and later as an assistant professor at the Department of Civil Engineering, BUET from 2015 to 2018. Mr. Azijul has more than 5 (five) years of professional, teaching and research experience in geotechnical and geo-environmental engineering. His research interests include ground improvement, foundation engineering, pavement materials, slope stability analysis and landslide prevention, and disaster management. Mr. Azijul has published in journals and conference proceedings. He has been serving as a reviewer in reputed international journals. He was awarded “Outstanding Civil Engineering Ph.D. Student” in recognition of academic excellence in Civil Engineering in 2018-19 and 2019-20 session. He wants to pursue his career in research and teaching profession. Faria Fahim Badhon is a Ph.D. candidate in the Civil Engineering Department at the University of Texas at Arlington. Faria has completed her Bachelor of Science in Civil Engineering and Master of Science in Civil & Geotechnical Engineering from Bangladesh University of Engineering & Technology (BUET) in 2015 and 2018, respectively. She has more than 5 (five) years of professional experience in geotechnical and geo-environmental engineering. She has extensive research experience on bioengineering of slope stabilization techniques during her M.Sc. thesis. Ms. Faria worked as a lecturer in Presidency University from 2015 to 2016. She worked as an assistant engineer in Bangladesh Water Development Board from 2016 till joining to UTA. As a Ph.D. student, Ms. Faria is now working on improving the bearing capacity of weak foundation soil using recycled plastic pins. She was awarded “Outstanding Civil Engineering Ph.D. Student” in recognition of academic excellence in Civil Engineering in 2019-20 session.
Faria Fahim Badhon is a Ph.D. candidate in the Civil Engineering Department at the University of Texas at Arlington. Faria has completed her Bachelor of Science in Civil Engineering and Master of Science in Civil & Geotechnical Engineering from Bangladesh University of Engineering & Technology (BUET) in 2015 and 2018, respectively. She has more than 5 (five) years of professional experience in geotechnical and geo-environmental engineering. She has extensive research experience on bioengineering of slope stabilization techniques during her M.Sc. thesis. Ms. Faria worked as a lecturer in Presidency University from 2015 to 2016. She worked as an assistant engineer in Bangladesh Water Development Board from 2016 till joining to UTA. As a Ph.D. student, Ms. Faria is now working on improving the bearing capacity of weak foundation soil using recycled plastic pins. She was awarded “Outstanding Civil Engineering Ph.D. Student” in recognition of academic excellence in Civil Engineering in 2019-20 session. Tanvir Imtiaz is a Ph.D. candidate at the University of Texas at Arlington. Tanvir received his Bachelor of Science degree from Bangladesh University of Engineering & Technology (BUET), Dhaka, Bangladesh in 2017. He has been working as teaching and research assistant in the Civil Engineering Department of The University of Texas at Arlington since 2018. His research interest is in recycled pavement materials, microstructure analysis of recycled materials and reusing recycled plastic in pavement construction. Mr. Tanvir has published in different international journals and conferences. He was awarded “Outstanding Civil Engineering Ph.D. Student” in recognition of academic excellence in Civil Engineering in 2018-19 session. He also received 1st price in National Outreach and Engagement Photo Contest Organized by Geo-Institute of ASCE.
Tanvir Imtiaz is a Ph.D. candidate at the University of Texas at Arlington. Tanvir received his Bachelor of Science degree from Bangladesh University of Engineering & Technology (BUET), Dhaka, Bangladesh in 2017. He has been working as teaching and research assistant in the Civil Engineering Department of The University of Texas at Arlington since 2018. His research interest is in recycled pavement materials, microstructure analysis of recycled materials and reusing recycled plastic in pavement construction. Mr. Tanvir has published in different international journals and conferences. He was awarded “Outstanding Civil Engineering Ph.D. Student” in recognition of academic excellence in Civil Engineering in 2018-19 session. He also received 1st price in National Outreach and Engagement Photo Contest Organized by Geo-Institute of ASCE. The Department of Civil Engineering is fully committed to accommodate all students with online instructions with different modalities during COVID 19 and beyond. This Laboratory Manual is the state-of-the-art online instructional manual for “Properties and Behavior of Soil” published by MAV Open Press.
The Department of Civil Engineering is fully committed to accommodate all students with online instructions with different modalities during COVID 19 and beyond. This Laboratory Manual is the state-of-the-art online instructional manual for “Properties and Behavior of Soil” published by MAV Open Press.