Urban Form and Land Use – Transportation Interactions

Qisheng Pan; Soheil Sharifi

4 Urban Form and Land Use – Transportation Interactions

Chapter Overview

Chapter 4 discusses the relationship between transportation, land use, and urban form. It identifies and explains different urban forms: monocentric, polycentric, clustered, and dispersed. It describes observing and delineating a metropolitan area by identifying major components such as traffic analysis zones (TAZs) and transportation networks. Additionally, this chapter addresses how different activities and land uses are distributed across the region, shaping different structures of cities and regions including monocentric and polycentric urban forms. The chapter discusses two case studies, Houston and Calgary, and highlights the empirical model as a well-established econometric model.

Learning Objectives

Type your learning objectives here.

Explain and compare various urban forms and their impact on the distribution of activities and travel patterns.
Explain the methods and metrics for quantifying urban form and density.
Recognize and explain the empirical modeling approaches for analyzing the interaction between land use and transportation.

INTRODUCTION

As described in Chapter 2, the initiation of land use and transportation modeling occurred in the 1960s and 1970s, driven by the availability of large computers that enabled the execution of extensive, though simple, digital simulations. These simulations were necessary to meet federal planning requirements and qualify Metropolitan Planning Organizations (MPOs) for federal funding. The four-step travel modeling approach emerged during this period, primarily driven by concerns about congestion reduction and air quality. The theoretical foundations of these models, discussed in Chapter 3, trace back to 19th-century and early 20th-century urban economics and geography, incorporating influences from physics and mathematics. The original top-down approach underwent a transformation in the 1990s, shifting to a bottom-up approach in response to the policy analysis needs imposed on MPOs by local governments and citizen groups. These demands included the necessity to model the land-use effects of transportation plans and micro-simulate the travel behavior of all households and firms. These developments highlight the importance of accurately representing the urban area’s economic structure and accessibility features in land-use transportation interaction modeling.
This chapter further delves into various urban forms and spatial structures within urbanized areas, introducing some econometric models for land-use transportation interaction modeling. This is a critical component of landuse/transportation modeling as urban form can have several implications for travel behavior and interactions of agents and activities in urban landscape. For instance, smart growth is a land use policy defined at both regional and local levels to influence travel patterns by affecting travel choices such as destination or mode choice. Urban form can be defined at various levels including strategic or regional (relative location of city, size of the city, or land use types), local (agglomeration, clustering, land use mix) or neighborhood (density, diversity, network layout). However, a lot of these variables can be defined and used at other levels too (Stead & Marshall, 2001). Thus, in this chapter we limit our focus to studies of urban form and present findings and ideas of previous studies that has informed land use and transportation modeling.Spatial analysis constitutes a fundamental aspect of land use and transportation modeling, providing insights into the relationship between transportation systems and urban forms. This form of analysis enables the identification of activity distribution and characteristics within urban areas. To initiate an integrated analysis of land use and transportation, a comprehensive understanding of spatial arrangements and infrastructure, including road networks, employment centers, and housing, is essential. The following components are crucial for this type of modeling:

Study area: Clearly delimit the geographical extent(s).
Zones: Divide the study area into a set of zones.
Existing transportation system: Construct a network model based on the existing transportation systems.
Zone identification: Create and represent similar areas, such as Traffic Analysis Zones (TAZs), using points or nodes (centroids).
System links: Connect the zone centroids through the transportation links.

Once these steps are taken, it becomes possible to predict travel behavior patterns and their relationship with transportation elements such as modes and networks (Clark, 1975).

Components of Land-use/Transportation Analysis Spatial Analysis

The classical land-use transportation interaction model of Wegener and Fürst (1999) depicted in Figure 4.1 shows a continuous loop of interactions among the four major components: accessibility, land use, activity, and transportation. Wegener and Furst (1999) also identified five key parameters within the land use component that significantly impact urban mobility patterns. These land use parameters are summarized by Le Néchet (2012, n.p.) as:

Density of specific types of land use in an urban area:

Residential land use density of the urban area likely to affect the modal share of transit.

Density of jobs, typically with complex impacts on commuting distance depending on the jobs/housing balance:

Longer distance if poor jobs/housing balance
Shorter distance if good jobs/jousting balance

Local/neighborhood urban form potential to influence modal choice particularly walking and cycling modes (Lin & Yang, 2009).
Population and the size of the city influence on level of transit use (proven to induce more transit trips and shorter trips).
“Location factor” based on the overall structure of the city (Le Néchet, 2012).

Figure 4.1 shows a loop in which four components of transportation and land-use modeling play pivotal roles.

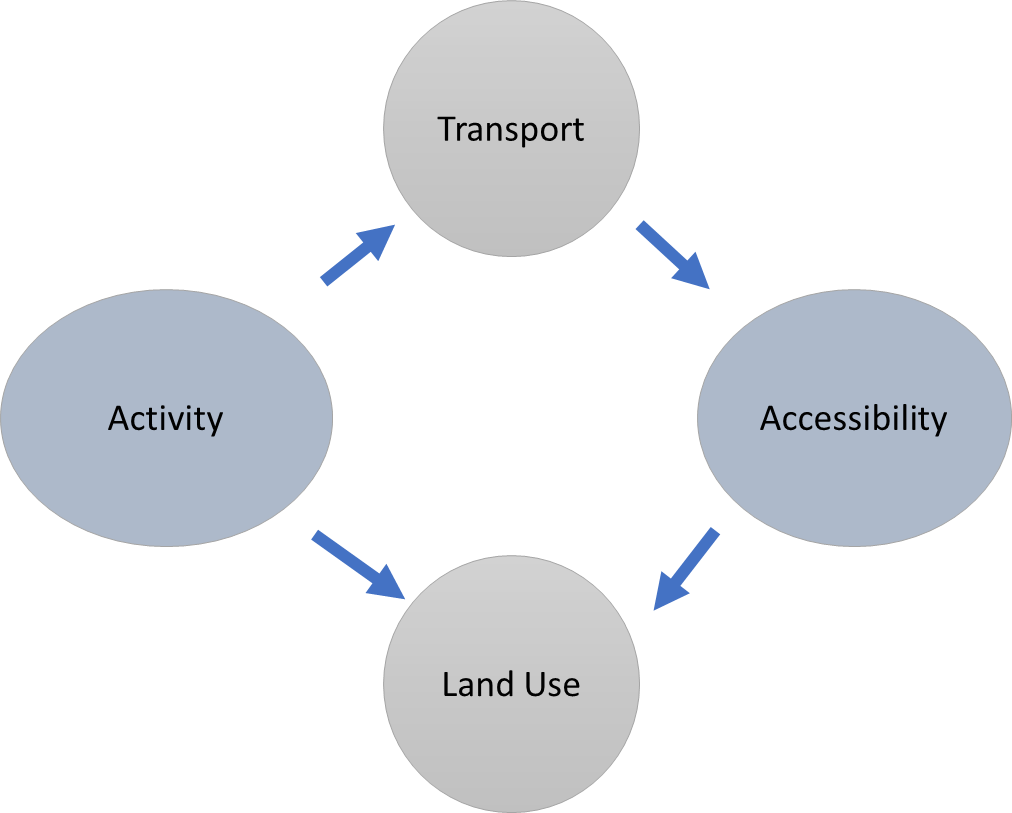
relationship of land use, transport, activities and accessibility — **Figure 4.1** The relationship between land use and transportation. From “Monitoring the Impact of Large Transport Infrastructure on Land Use and Environment Using Deep Learning and Satellite Imagery,” by M. Pavlovic et al., 2022, Remote Sens, 14(10), p. 3. CC BY 4.0.

The land use parameters outlined in Figure 4.1 are crucial for informing urban planning and design. These parameters play a vital role in efficient and sustainable mobility patterns. They can significantly influence transportation patterns and modal choices.

Residential density, especially when combined with shorter trips, is likely to promote the use of public transport. The density of jobs can have complex effects on commuting distances, leading to longer distances if jobs are concentrated in a small number of centers. Conversely, a balance between residential areas and places of employment, especially with an increase in transport costs, is likely to result in shorter commuting distances.

The local urban form also plays a role in shaping modal choices, particularly for soft modes like walking and cycling. The size of the city is another factor, with more populated cities associated with shorter travels and a higher use of transit. Overall urban form and location are crucial in influencing transportation patterns and modal choices.

In addition to the factors depicted in Figure 4.1, other complex elements such as economic, political, demographic, and technological changes play a role in the spatial form of cities and transportation systems. Recent technological advancements have greatly influenced travel and mobility patterns in urban areas. For example, digitalization has facilitated on-demand ride-sharing services like Uber and contributed to decreased travel needs by providing on-demand delivery services. Despite their transformative potential, these innovations have had a considerable impact on mobility patterns. Economic factors, such as income levels, can also influence daily trips in terms of timing, destination choice, and mode. Therefore, analyzing the spatial structure of urban areas, including the activities of different socio-demographic groups, informs the model (Zhang, Cheng, and Aslam 2019).

Urban Spatial Structures

To better understand the spatial structure of cities and regions, we can classify different city forms based on the concentration of value-added activities such as retail, manufacturing, and distribution services. The two broad classifications are:

Centralization Centralization refers to the advantages of organizing various activities in the central city, in which the accessibility in the core is the highest by far. (Recall Von Thünen’s model of a monocentric city.)

Clustering is another driving force of location choice and spatial structure, which refers to the proximity of (primarily similar) activities to each other due to the benefits of agglomeration (Boarnet, Hong, and Santiago-Bartolomei, 2017).

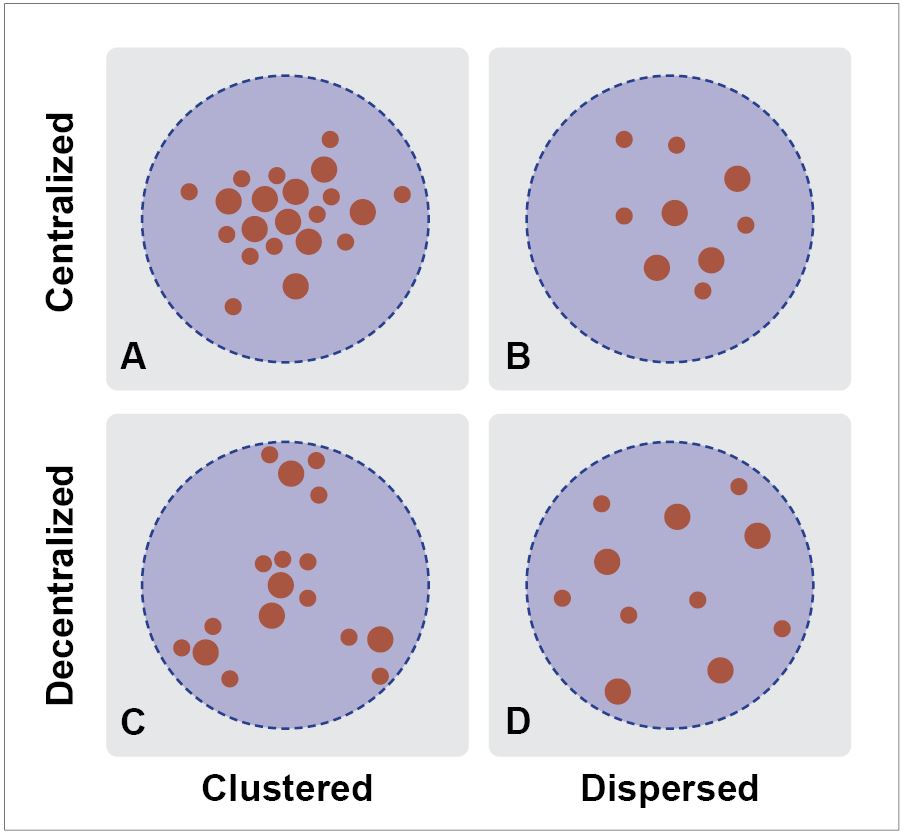
Figure 4.2 illustrates how the four major types of spatial structures are formed, resulting from a combination of clustering and centralization.

The first one (type A) is a centralized form that accommodates most activities in the city’s central place, and these activities enjoy the benefits of agglomeration.
Another frequently observed structure is decentralized, in which clustering is still a predominant feature (type C), but clustered in some locations in the region.
There is also a wholly dispersed structure with no clustering and centrality (type D).
Additionally, (type B) is a centralized form, but the central places are dispersed and have formed clusters in specific locations (Rodrigue 2020).

distribution of activities (four types); centralized, decentralized, clustered and dispersed. — **Figure 4.2** Urban spatial structures according to agglomeration. From The geography of transport systems, p.220 by Rodrigue, 2020 New York. Copyright 2022 by Routledge.

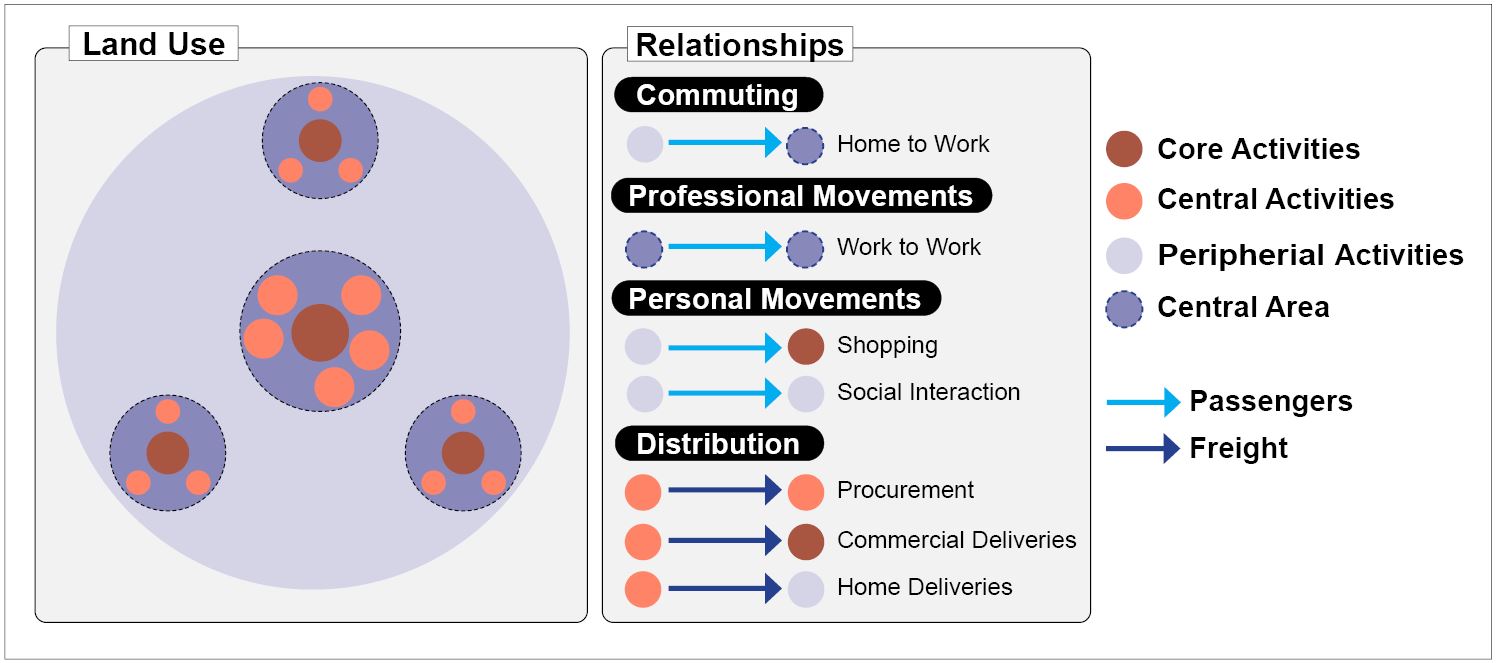
Once the general spatial structure of urbanized areas is classified, the next step is to consider how the various zones and areas, such as urban cores, residential or commercial zones, and different land uses, interact. As previously discussed, recognizing the reciprocal impact of land uses and travel patterns is a crucial aspect of modeling land-use and transportation interactions. It is presumed that each land-use zone, with its unique features, forms specific relationships with other zones. The interplay between land use and transportation is reflected in the mobility and accessibility of both passenger and freight movement, representing travel demand and cost between these zones. Therefore, it is essential to closely examine different types of zones, particularly those exhibiting consistent patterns of trip generation and attractions, such as Central Business Districts (CBDs), residential areas, and major commercial, manufacturing, and transport hubs like train stations, airports, and harbors.

Western cities often exhibit a typology characterized by several rings of activities surrounding a central core. The core area, known as the Central Business District (CBD), typically hosts activities like office headquarters, banks, insurance, and financial companies, providing a high level of accessibility. The next layer, referred to as main activities, surrounds CBDs and attracts warehousing, wholesale, and manufacturing activities due to their need for accessibility and substantial land consumption. The outermost ring accommodates peripheral activities, where a mix of residential lands and local services coexist. According to this structure, we can predict mobility patterns between these zones. Figure 4.3 depicts the three primary relationships between zones (Rodrigue 2020).

Commuting is the first and most common kind of travel that occurs primarily between residential areas and CBDs (workplaces) and is important for land use and transportation modeling.
The second type of mobility pattern is called professional movements. It mainly concerns work-based movements between workplaces within central areas or clusters.
Personal movements include various activities such as social gatherings, leisure trips, and shopping trips.
Distribution is the last category, in which freight movement and distribution are the main goals of such trip generations. Online shopping, deliveries, and distributing raw materials to manufacturing clusters are among the different activities in this category. Figure 4.3 depicts the relationship between land uses just described (Rodrigue 2020).

distribution of activates and movements; commuting, professional movement, and personal movement. — **Figure 4.3** Relationship between land use and various trip purposes. From The geography of transport systems, p. 327,by Rodrigue, 2020, New York. Copyright 2022 by Routledge.

The Spatial Evolution of Urban Travel

Monocentric cities, characterized by a central area attracting most daily trips from peripheral regions, have historically been prevalent. However, empirical evidence reveals that cities often do not conform to a monocentric form, and various clusters emerge due to factors such as the development of smaller secondary employment centers. These patterns introduce complexity to the traditional travel routes from residential areas to the central business district (CBD).

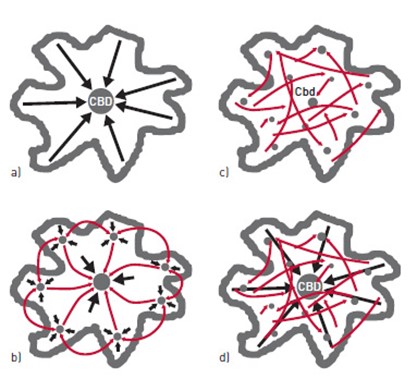
Bertaud (2021) classifies urban travel spatial distribution into four types based on the urban form, as illustrated in Figure 4.4:

Monocentric Form: This is the oldest observed form, featuring a unified commuting pattern from peripheral areas to the center via diagonal and radial roads or rail stations for workers. In this form, a negative density gradient from the center to peripheral areas is observable, provided land-use regulations and zoning laws allow such a pattern (Figure 4.4a).
Polycentric Cities (Urban Villages): Representing an ideal form from an urban planning perspective, polycentric cities allow for shorter and more accessible trips to multiple centers of work and services. The congregation of centers as self-supporting urban villages forms a low-density and sprawled city, where alternative transportation modes like walking or biking become more viable for various trip purposes (Figure 4.4b).
Auto-centric Urban Form: Despite the ideal short trips to clusters in polycentric cities, this form often becomes auto-centric. Dwellers of sub-centers (satellite towns) frequently commute to the city center for job opportunities, resulting in a polycentric urban form with quasi-“Brownian” movement (Figure 4.4c).
Polycentric Cities (Central City Jobs): The transformation of monocentric urban forms into polycentric ones occurs gradually due to physical growth accommodating population and economic growth, leading to the formation of urban clusters. In this form, the CBD loses its central dominance, secondary clusters attract trips, and a consistent trip distribution pattern throughout the urbanized area can be observed (Figure 4.4d). Various factors, such as a historical center with few amenities, a high motorization rate, low land cost, flat topography, or a grid-like street network, may accelerate this evolution. Once achieved, this urban form generates new trip generators and attractors, scattering them across the entire city (Lefèvre, 2009).

flows of trips (origins and destinations) under four different urban forms. — **Figure 4.4** Trip patterns within various urban structures. From “Urban Transport Energy Consumption: Determinants and Strategies for its Reduction. An analysis of the literature,” 2009, by B. Lefèvre, B,, SAPIENS: S. Surveys and Perspectives Integrating Environment and Society, (2.3), p.6. CC BY 4.0.

Urban Structure Quantification

Over time, monocentric cities deviate from their centralized growth pattern, giving rise to the formation of subcenters and the transition into polycentric urban structures. The clustering of economic activities in multiple centers, either through concentration or relocation, is a key factor driving the evolution of modern cities. Empirical studies indicate the prevalence of polycentric city formations in both new and established urban areas. The identification of these subcenters is influenced by their definition, and they may not always manifest as distinct points but can cluster along significant roads.

Subcenters, whether in the form of corridors or specific points, play a crucial role in understanding their surroundings in various aspects, including population rate and density, employment rate and density, as well as land values (Agarwal, Giuliano, and Redfearn, 2012).

Three formulas have been used to quantify the transformation of a monocentric city into a polycentric one. All three formulas share a common origin, stemming from the general negative exponential function D(x) = Ae^(-γx). However, each formula is based on a different assumption regarding how the occupant of a land parcel values access to multiple centers. In this fundamental function, D(x) represents the density at location x, where x is the distance from the center, and A and γ are positive constants.

The first formula assumes that each center generates its own declining bid-rent function for surrounding land. In other words, what matters at any point is only the center with its most significant influence on that point. Since this model is not frequently seen in empirical cases, it is rarely used in applied work” (Anas, Arnott, and Small 1998, p.22).

$D_m=Max_n⁡{A_n exp⁡(-(y_n.x_m_n) )}$

Where $D_m$ is density at location m, $x_m_n$ is distance of location m to center n, and A, An, and $y_n$ are coefficients to be estimated.

2. The second formula assumes that centers are complements. The occupant of a given location requires access to every center” (Anas, Arnott, and Small 1998, p.22). A problem with this algorithm is that at a great distance from even one subcenter, development at location m can be completely prevented according to the model. A good modification for overcoming this problem is to replace – γn. xmn with γn/ xmn.

$D_{M}= A \prod_{n-1}^{n}(exp⁡(-(y_n.x_m_n) )$

3. The third formula (Small and Song 1994; Gordon, Richardson, and Wong 1986) assumes that the accessibility of a location is determined by the sum of exponentially declining influences from various centers” (Anas, Arnott, and Small 1998, p.23).This formula is similar to the previous one, but unlike it, a center’s influence becomes negligible at large distances.

$D_{M}= A \sum_{n-1}^{n}(exp⁡(-(y_n.x_m_n) )$

Each of the three formulas designed to construct a density gradient relies on theoretical assumptions, and their applicability is constrained by specific contexts. The impact of subcenters on adjacent centers and locations, along with the interrelationships and development patterns concerning the central area, may vary across different cities. To determine the most suitable function for describing the density of a city or region, an empirical understanding or a comprehensive review of the existing literature is essential.

Empirical Econometric Model

Urban and regional economic models explain and simulate the economic conditions of a city or region in terms of population and employment growth. Such outputs can be exerted as inputs for subsequent models in which other forecasting variables like land use is the goal. These economic models can also help us identify and explain the impact of inter-metropolitan growth. Some of these models can only predict employment growth, while others include employment and population in the model. For the rest of this chapter, we elaborate on the empirical econometric model developed around the 1960s by a traffic research corporation for the Boston regional planning project (Parsons, Brinckerhoff, and Quade & Douglas 1999).

The general structure of the empirical model consists of m activities (1,2,3,….,i,…,m) and n subareas (1,2,3,…,j,…n). The model’s primary goal is to predict the distribution of each of the m activities to the n subareas at the end of the forecasting year (time period). The model utilizes the predicted change in the subarea share of each of the activities over the forecasting period to predict the activities’ distribution. The formula for calculating the change in the subarea share of activity between times t-1 and t is as follows:

$S_{ij} = \frac{E_{ijt}}{\sum_{j} E_{ijt}} - \frac{E_{ij(t-1)}}{\sum_{j} E_{ij(t-1)}}$

Where

$S_ij$ is the change in the subarea share of activity i for subarea j,

$E_ij$ is the level of activity I in subarea j

One of the main assumptions in this model is that the changes in subarea shares of the activities are determined simultaneously. The change in the subarea share of activity is assumed to be proportional to (1) the change in the subarea share of each of the other activities, and (2) the subarea share, or change in the subarea share, of several variables describing certain characteristics of a subarea, for example, accessibility, income, vacant land, etc. The equation that represents the mentioned conditions can be written as

$S_{ij} = \sum_{q \neq i} a_{iq} S_{qj} + \sum_{k} b_{ik} (X_{kj} \text{ or } Z_{kj}), i=1,2,…,m$

where

$S_ij$ is the change in the subarea share of activity i in subarea j

$S_qj$ is the change in the subarea share of activity q in subarea j

$X_kj$ is the change in the subarea share of a variable representing the kth characteristic of subarea j

$S_zk$ is the subarea share of a variable representing the kth characteristic of

subarea j

$a_iq$ is the parameter corresponding to the qth variable in the ith equation

$b_ik$ is the parameter corresponding to the kth variable in the ith equation

Since the model is mainly concerned with changes in variables over time, we need to obtain data for two past points to calculate the variables’ weights or coefficients. To run the model, we use a technique called simultaneous linear regression. With all the parameters available for each variable, the model can be used to make forecasts. We can determine changes in the share of activities in subareas by using the reduced form equation of simultaneous linear regression and inputting the values that represent the subarea’s characteristics. Additionally, we can determine the total activity level in each area by adding up the predicted changes along with the initial share of activities (Stokes 1974).

The model was first developed for the Boston area (Hill, Brand, and Hansen, 1966). Since then, it has been applied to several areas to study the impact of public investment in infrastructure on differential growth among zones. In the original application of the model in the Boston area, the main intention was to analyze the impact of transportation investments. This model has also been used for other metropolitan areas such as Washington, D.C., Minneapolis, Denver, and various Canadian cities. In this model, the variables are classified as endogenous and exogenous. The former or X variables represent the levels, rates of change, or shares of different land uses and activities estimated within the model. The latter, or the Z category, denotes the levels or rates of changes in exogenous factors like policy instruments. For instance, the Z variables may represent the level of investments for various infrastructure projects. X variables are land uses and activity responses to such investments over a specific period.

In terms of its limitations, this model overlooks the interactions among different zones, relying solely on exogenous variables to determine each zone’s endogenous variables. Furthermore, the model lacks an inherent mechanism to ensure that the estimation of endogenous variables will not be negative. Negative values would be meaningless in this context. To address this, an ad-hoc procedure is required to adjust these forecasts to sum to a predetermined total, which must be independently forecasted (Anas, 2013).

In the subsequent sections of this chapter, we will delve into two real-world applications demonstrating accessibility and urban spatial structure. Additionally, we will explore a real-world application of the empirical model in the context of the Calgary Metropolitan Area.

Case studies

Houston

Pan, Jin, and Liu (2021) extended Hansen’s accessibility formula (described in Chapter 3.2.1) to incorporate socioeconomic factors and multi-modal transportation systems into job accessibility measures for understanding employment accessibility patterns in the Houston Metropolitan Area. Previous models seeking to measure accessibility to job opportunities only considered supply-side factors like job types and wage rates. Pan, Jin, and Liu’s (2021) model introduced demand-side variables like socioeconomic background, car ownership, and skills in their modified version of employment accessibility.

This study adopts a model for an employment accessibility measure that integrates competition on the demand side, matching jobs, and workers, combining multiple travel modes, and the socioeconomic characteristics of job seekers. The authors attempted to show the impacts of competition on employment accessibility and to what extent multi-modal transport may shape the distribution of employment accessibility differently. The authors also highlighted how matching jobs with job seekers of different economic and educational backgrounds could affect employment accessibility measurement. Figure 4.5 presents a conceptual framework that illustrates the relationship among accessibility, competition, and matching with the critical components of workers, jobs, and transportation in employment accessibility measures.

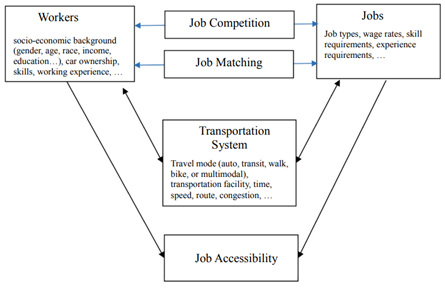
framework for adding job matching and competition in accessibility measurement — **Figure 4.5** Employment accessibility analysis with regard to job matching and competition From “Measuring the effects of job competition and matching on employment accessibility” by Pan et al. 2020, *Transportation Research Part D: Transport and Environment*, *87,* p.2.

Model Development

Accessibility is defined as the potential of opportunities for interaction (Hansen 1959), the expected maximum utility that an individual derives from a given situation (Weisbrod, Lerman, & Ben-Akiva, 1980), or the ease of reaching destinations, such as workplaces. A general form of Hansen’s formula to estimate the spatial interaction of opportunities is presented below:

$A_i=∑_jO_j f(C_ij )$

where Ai is accessibility of zone i for a given type of opportunities. Oj is the quantity of a given type of opportunities in zone j, such as jobs, population, shops. Cij is travel cost from zone i to zone j. f (Cij) is impedance function that measures the interaction between zone i and zone j. As we discussed, Hansen’s model only captures the supply side of the job competition issue and thus fails to incorporate individual preferences, ignores demand factors, and does not consider job competition and matching. Shen (1998) was the first person to add the demand component to the accessibility framework using the following formula:

$D_j=∑_k S_k f(C_kj )$

where Sk is the number of opportunity seekers living in zone k, and f (Ckj) is impedance function that measures the interaction between zone k and zone j. Thus, the Hansen formula can be rewritten as follows:

$A_i^m=∑_j (O_j f(C_ij^m ))/(∑_n D_j^n ) " or"$

$A_i^m=∑_j (O_j f(C_ij^m ))/(∑_n ∑_k S_k^n f(C_kj^n ) )$

where Ai m is accessibility from zone i to a given type of opportunities through mode m. Sk n is the number of opportunity seekers living in zone k and traveling by mode n. Dj n is the demand of opportunity seekers in zone j and traveling by mode n. f (Cij) m and f (Ckj) n are the impedance functions for traveling from zone i to zone j in mode m and traveling from zone k to zone j in mode n, respectively. the additional refinement in this study includes incorporating the matching of the socio-economic backgrounds of opportunity seekers to the specific type of opportunities. The modified model developed by Pan, Jin, and Liu (2020) can be written as follows:

$A_i^{(m,t)} = \sum_j \frac{O_j^t f(C_{ij}^m)}{\sum_n D_j^{(n,t)}}$

$A_i^{(m,t)} = \sum_j \frac{O_j^t f(C_{ij}^m)}{\sum_n \sum_k S_k^{(n,t)} f(C_{kj}^n)}$

where Ai m,t is accessibility in zone i for the opportunities of type t through mode m. Oj t is the number of opportunities of type t in zone j. Dj n,t is the demand of opportunity seekers matching to the opportunities of type t, residing in zone j, and traveling by mode n. Sk n,t is the number of opportunity seekers matching to the opportunities of type t, residing in zone k, and traveling by mode n.

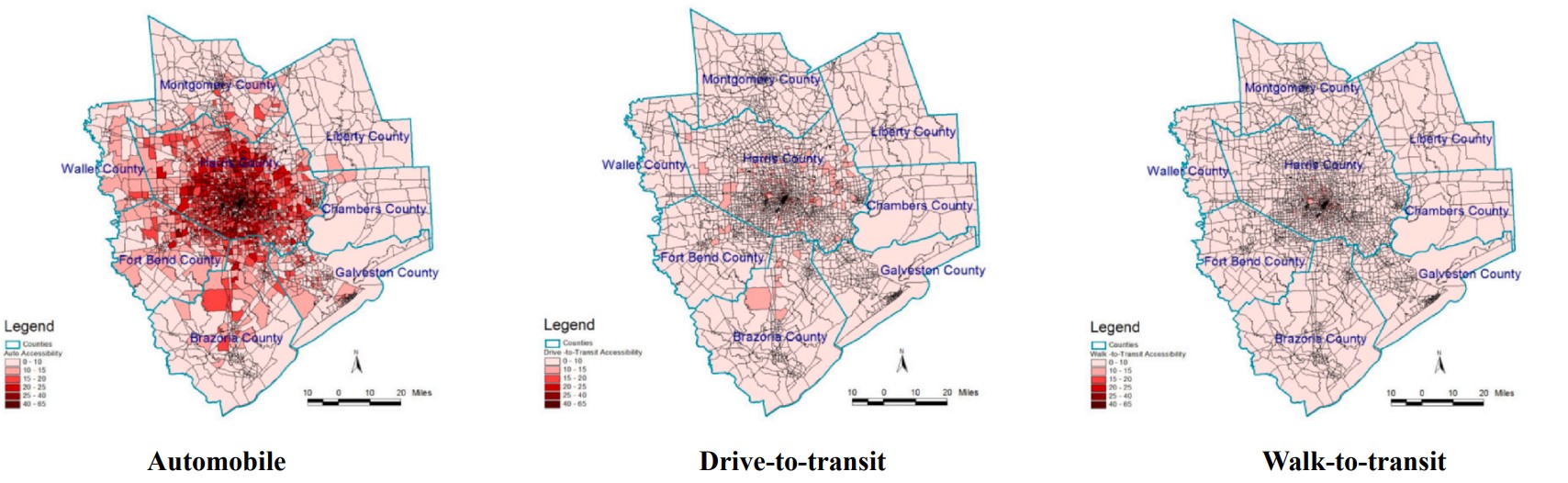
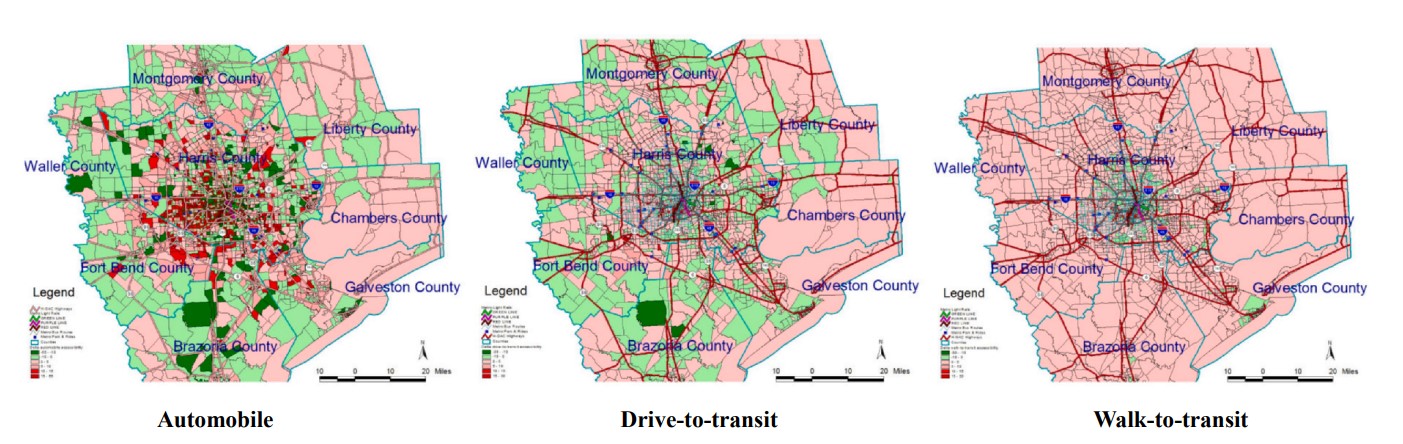
It should be noted that the travel impedance function for this study is derived from (Wilson 1971) negative exponential functions e Cij (where, > 0). The friction factors for the home-based-work (HBW) trips are derived from the travel time distribution for each type of mode. The results of the study clearly show that first employment opportunities are more concentrated in the downtown area of the city and the accessibility pattern for the three modes of transit shows outstanding divergence among one another. Figure 4.6 compares job accessibility for three different commuting modes.

The input data for this analysis are a 2015 O-D trip matrix and peak-hour travel time matrix from H-GAC, the socio-economic data from the 2009–2013 ACS, and job information from H-GAC and 2014 InfoGroup Business Data. The model used in this paper for measuring employment accessibility for job seekers who commute by automobile or transit to reach job opportunities matching their socio-economic background is:

$A_i^{\mathrm{Auto,t\ }}=\sum_j\hairsp\frac{O_j^tf\left(C_{ij}^{\mathrm{auto\ }}\right)}{\sum_k\hairsp\left[\alpha_kS_k^tf\left(C_{kj}^{\mathrm{auto\ }}\right)+\left(1-\alpha_k\right)S_k^tf\left(C_{kj}^{\mathrm{tran\ }}\right)\right]}$

$A_i^{\mathrm{Tran,t\ }}=\sum_j\hairsp\frac{O_j^tf\left(C_{ij}^{tran}\right)}{\sum_k\hairsp\left[\alpha_kS_k^tf\left(C_{kj}^{\mathrm{auto\ }}\right)+\left(1-\alpha_k\right)S_k^tf\left(C_{kj}^{\mathrm{tran\ }}\right)\right]}$

$A_i^{\mathrm{drvtotran,t\ }}=\sum_j\hairsp\frac{O_j^tf\left(C_{ij}^{\mathrm{drvtotran\ }}\right)}{\sum_k\hairsp\left[\alpha_kS_k^tf\left(C_{kj}^{\mathrm{auto\ }}\right)+\left(1-\alpha_k\right)\beta_kS_k^tf\left(C_{kj}^{\mathrm{drtotran\ }}\right)+\left(1-\alpha_k\right)\left(1-\beta_k\right)S_k^tf\left(C_{kj}^{\mathrm{walktotran\ }}\right)\right]}$

$A_i^{\mathrm{walktotran,t\ }}=\sum_j\hairsp\frac{O_j^tf\left(C_{ij}^{\mathrm{walktotran\ }}\right)}{\sum_k\hairsp\left[\alpha_kS_k^tf\left(C_{kj}^{\mathrm{auto\ }}\right)+\left(1-\alpha_k\right)\beta_kS_k^tf\left(C_{kj}^{\mathrm{drvtotran\ }}\right)+\left(1-\alpha_k\right)\left(1-\beta_k\right)S_{kj}^tf\left(C_{kj}^{\mathrm{walktotran\ }}\right)\right]}$

$A_i^{All,t}=\alpha_iA_i^{Auto,t}+\left(1-\alpha_i\right)_i^{\mathrm{Tran,t\ }}$

$A_i^{All,t}=\alpha_iA_i^{Auto,t}+\left(1-\alpha_i\right)\beta_iA_i^{\mathrm{drvtotran\ },t}+\left(1-\alpha_i\right)\left(1-\beta_i\right)A_i^{\mathrm{walktotran,\ }t}$

where A_i^{Auto, t} , A_i^{Tran, t} , A_i^{Drvtotran, t} , A_i^{Walktotran, t} ,and are employment accessibility from zone i to the opportunities of type through mobile, transit, drive-to-transit, and walk-to-transit mode, respectively.

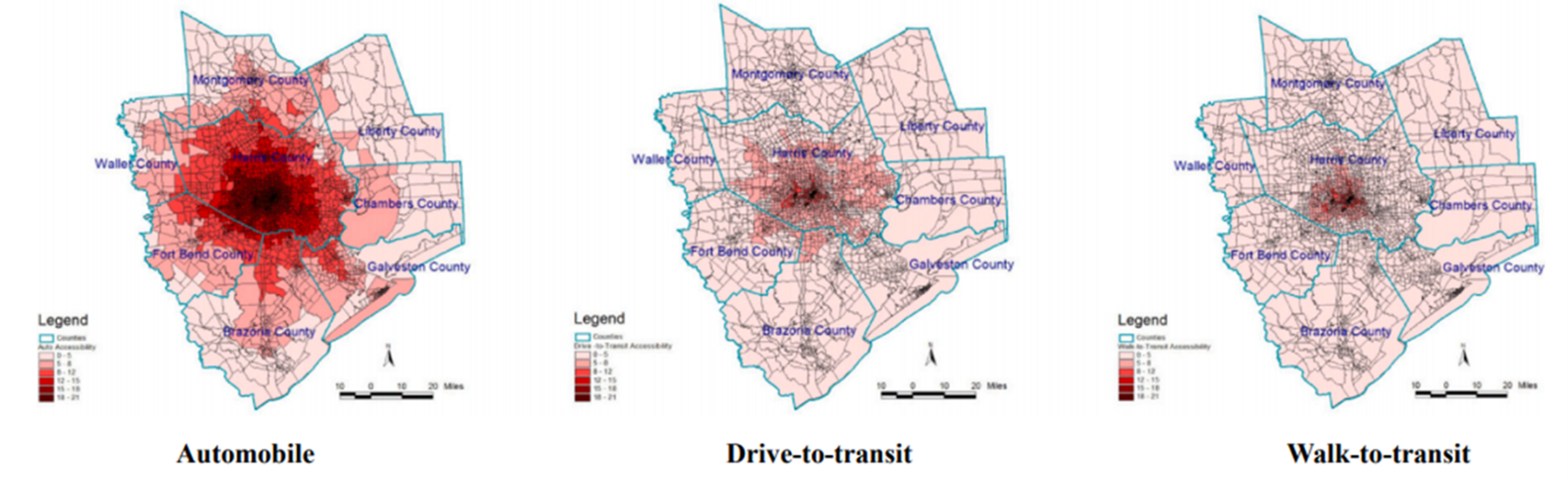
accessibility map for automobile, drive-to-transit and walk-to-transit. — **Figure 4.6** Employment accessibility by TAZ by job seekers by commuting modes. From “Measuring the effects of job competition and matching on employment accessibility” B by Pan et al. 2020, Transportation Research Part D: Transport and Environment, 87, p.11.

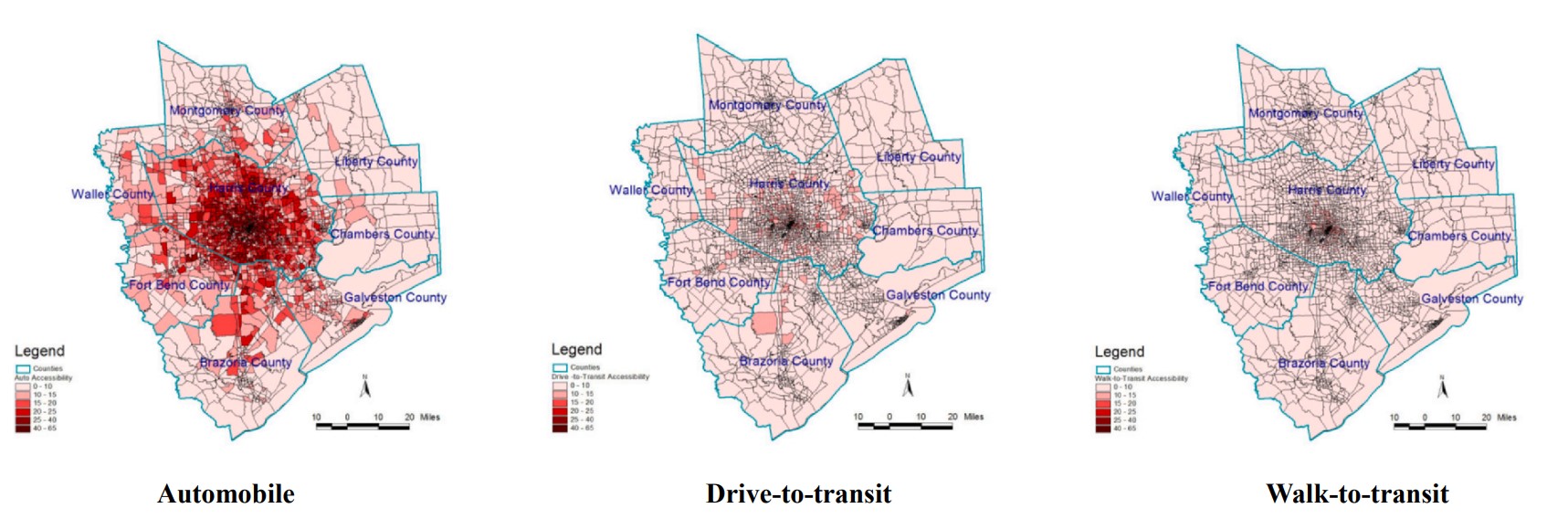
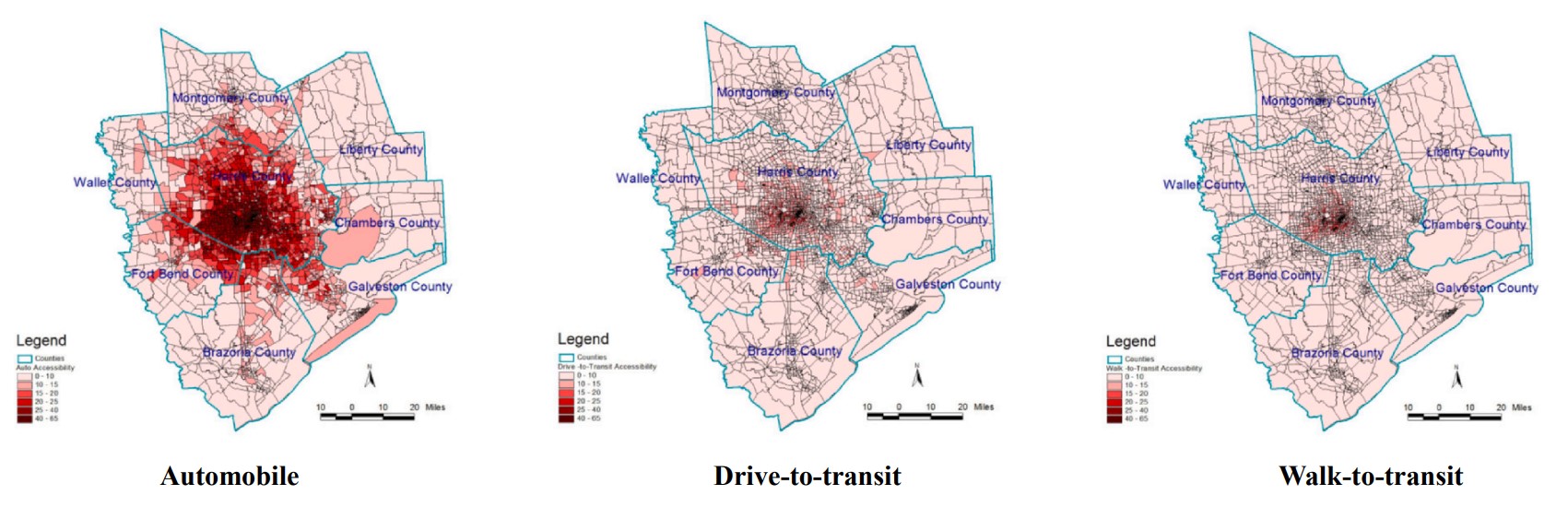
Additionally, in this study, the impact of the population in poverty and job seekers’ educational background is also investigated, and the results show that such factors undeniably affect job accessibility measurements. These factors should be incorporated in accessibility analysis studies. Figures 4.7, 4.8, 4.9, and 4.10 show the geographical variations in accessibility rates based on different income levels and educational backgrounds.

Accessibility map for automobile, drive-to-transit and walk-to-transit for below poverty workers. — **Figure 4.7** Employment accessibility by different modes for below poverty people Figure 4.6 Employment accessibility by TAZ by job seekrs by commuting modes From “Measuring the effects of job competition and matching on employment accessibility” By Pan et al. 2020, *Transportation Research Part D: Transport and Environment*, *87,* p.12.

**Figure 4.8** Employment accessibility by education attainment Figure 4.6 Employment accessibility by TAZ by job seekrs by commuting modes From “Measuring the effects of job competition and matching on employment accessibility” By Pan et al. 2020, *Transportation Research Part D: Transport and Environment*, *87,* p.13.

Accessibility measurement for three modes for blue collar jobs. — **Figure 4.9** Employment accessibility by education attainment Figure 4.6 Employment accessibility by TAZ by job seekers by commuting modes From “Measuring the effects of job competition and matching on employment accessibility” By Pan et al. 2020, *Transportation Research Part D: Transport and Environment*, *87,* p.13.

Accessibility measure differences for three modes between white and blue collar jobs. — **Figure 4.10** The difference of employment accessibility between transit job seekers with associate’s degree or above and those with high school degree or lower in multiple commuting modes. By Pan et al. 2020, *Transportation Research Part D: Transport and Environment*, *87,* p.13.

The Calgary Empiric Model

The next case study is from Calgary, Canada. This case study used six equations to predict the share of economic activities. Each formula corresponds to the following activities:

Population
Construction employment (U.S. code 2)
Manufacturing employment (U.S. code 3)
Transportation, communication, and other public utility employment (U.S. code 4)
Retail and wholesale employment (U.S. code 5)
Service employment (U.S. codes 6, 7, and 8). The study area was divided into sixty-eight sub- areas, and the statistical technique used for this study was three-step least squares. The equations associated with each of the mentioned economic activities are as follows:

$S_{\text{popj}} = 0.087S_{rwj} - 0.399E_{popj} + 0.256Y_{j} + 0.00043\log H_{popj}$

$S_{mj} = 0.38E_{mj} + 0.059H_{bj} + 0.356A_{ej}$

$S_{\text{tcpj}} = -0.249E_{\text{tcpj}} + 0.089H_{bj} + 0.182A_{ej}$

$S_{\text{rwj}} = 0.163S_{\text{popj}} + 0.26S_{mj} - 0.429E_{\text{rwj}} + 0.406A_{\text{popj}}$

where

$S_{\text{popj }}$ – is the change in subarea j’s share of population,

$S_{mj}$ – is the change in subarea j’s share of manufacturing employment,

$S_{\text{tcpj}}$ – is the change in subarea j’s share of transportation, communication, and other public utilities employment,

$S_{\text{rwj}}$ – is the change in subarea j’s share of retail and wholesale employment,

$S_{sj}$ – is the change in subarea j’s share of service employment,

$S_{\text{conj}}$ is the change in subarea j’s share of construction employment,

$E_{\text{popj}}$ is the base-year share of population in sub-area j,

$E_{mj}$ is the base-year share of manufacturing employment in sub-area j,

$E_{\text{tcpj}}$ is the base-year share of transportation, communication, and other public utilities employment in sub-area j,

$E_{\text{rwj}}$ – is the base-year share of retail and wholesale employment in sub-area j,

$E_{sj}$ is the base-year share of service employment in sub-area j,

$Y_{j}$ is the base-year share of mean family income in sub-area j,

$H_{\text{popj}}$ is the base-year holding capacity of vacant land for population in sub-area j,

$H_{bj}$ – is the base-year share of holding capacity of vacant land for industrial employment in sub-area j,

$A_{\text{popj}}$ is the base-year share of accessibility to population in sub-area j,

$δA_{\text{popj}}$ is the change in sub-area j‘s share of accessibility to population,

$A_{ej}$ is the base-year share of accessibility to total employment in sub-area j.

In this study, the conventional Hansen (1959) formula is utilized to measure accessibility. The model’s forecasting ability is assessed by comparing its predictions for changes in the share of activities with the actual changes and extrapolations for the specified time. The modeler substitutes observed values of predetermined variables for the 1964-1971 period into the model to generate predictions of endogenous variables, which are then compared with the observed values. The root-mean-square (RMS) technique is employed for this comparison, as indicated by the formula below:

where n is the number of Pi’s or Ai’ s. When the RMS = 0, there is equality between all the Pi’s and Ai’ s, that is Pi = Ai for all i. This is the case of perfect forecasting. The value of RMS increases as the accuracy of the predictions decreases.

$RMS=[1/n∑(P_i-A_i )^2 ]^(1/2)$

The change in the share of activities for two time periods, representing the model output, is summarized in the following table. Table 1 reveals that the model’s predictive accuracy for 1958-1964 is more precise and closely aligns with empirical data compared to predictions for 1964-1971. Challenges in predicting population growth in emerging residential areas in peripheral locations, along with underestimation of employment in manufacturing, transportation, and communication jobs, contribute to the lower accuracy in the latter period. Additionally, the model indicates a dispersion of retail and wholesale jobs in suburbia, contrary to the concentration observed in the CBD. The lower accuracy in the latter period is further attributed to model parameters calibrated using actual data from the former period. The study emphasizes that changes in relationships and the inclusion of new factors may alter variable interactions in the future, reducing model accuracy when using parameters from older data. According to Table 4.1, the most accurate estimation for both periods pertains to the population, as indicated by lower RMS values, signifying higher prediction accuracy.

**Table 4.1** The comparison between Calgary’s empirical model accuracy and errors for two time periods.
Note from “The evaluation of an Empiric model for an urban area” by Stokes, E., 1974. *Environment and Planning A*, 6(6), p.709.
Variable	Model	Simple extrapolations	blank cell
	R (1958-1964)	RMS	U	R (1964-1971)	RMS	U	R (1964-1971)	RMS	U
S (pop)	0.734	0-006	0.709	0-492	0-007	0.91	0-427	0-009	1.27
S(con)	0-503	0.01	0-855	0-031	0-011	1.104	-0.004	0.017	1.74
S(m)	0-672	0.01	0.741	0.361	0.01	1.045	0-100	0-017	1.84
S(tcp)	0.608	0-012	0.795	-0.029	0.019	1.09	-0.292	0.026	1.48
S(rw)	0.939	0.007	0-351	-0.602	0-016	2.334	-0.285	0-023	3.42
S(s)	0.917	0-010	0-401	-0.081	0-013	1.765	-0.141	0-027	3.66

Note from “The evaluation of an Empiric model for an urban area” by Stokes, E., 1974. Environment and Planning A, 6(6), p.709

The model’s predictive accuracy is deemed unsatisfactory based on the observed results, and the predicted values lack validity for the Calgary Metropolitan Area. Several problems and shortcomings contribute to the inadequacy of the model’s performance in this specific context. Firstly, the economic activity classification employed in the study is deemed inappropriate for the intended goal. Combining light manufacturing and heavy manufacturing without distinct sections for each fails to capture the distinct characteristics of these activities, leading to unreliable results. Another significant flaw in the model is its failure to account for the impact of public policies on location choices. For instance, policies restricting urban development in peripheral areas to mitigate excessive public service provision costs are not considered, resulting in an overestimation of the population in outer regions compared to reality. Additionally, the model requires parameter calibration for each case study and time to ensure reliable and accurate results. In essence, the empirical model leans more towards being a statistical model, lacking the incorporation of behavioral considerations, such as policy effects. Consequently, the model’s predictions rely on historical trends rather than being derived from relevant theories (Stokes, 1974).

Conclusion

In this chapter, we explored the intricate spatial connections among activities, transportation infrastructure, land use, and population. The urban travel and mobility patterns, as revealed, are closely linked to the spatial structure and form of the city. Additionally, changes in urban structure, such as the emergence of new centers, the diminishing influence of central locations, and population growth in peripheral areas, can significantly impact land use and transportation models and their effectiveness.

Our case studies highlight the importance of considering the type of jobs and services when modeling spatial relationships. This is crucial because individuals, households, and businesses with different income levels exhibit varied travel and locational behavior, significantly influencing the distribution of opportunities and activities. Moreover, to rely on modeling results for future developments, it becomes essential to employ different models and various calibration methods. Throughout the four chapters, we have discussed both foundational and newer land use and transportation models.

Glossary

Econometric models are statistical models that are used for discovering statistical relationship between different quantities such as urban density.
Land use density refers to the amount of development that has taken place per a unit of space for a particular land use type under zoning regulations.
Centralization refers to the advantages of the central part of the city on organization of all activities, which are all under the influence of accessibility (recall the Von Thunen model of a monocentric city)
Clustering refers to proximity of (mostly similar) activities to each other due to the benefits of agglomeration
Decentralized form is an urban form in which activities are clustered around a corridor or a sub-center as opposed to centralized or dispersed from
Dispersed form is another urban form that the distribution of activities is fairly even across a city
Central Business District (CBD) refers to a commercial and business center of a city that also knows as city center or downtown.
Commuting is a round trip from home to work in the morning and from work to home in the evening time.
Professional movements is a type of mobility pattern that usually takes place between workplaces within central areas or clusters.
Personal movements is a type of mobility pattern that includes wide range of activities such as social gatherings, leisure trips, and shopping trips
Urban villages is a form of polycentric urban structure with medium-density, land use mix and good public transit.
Satellite towns are small municipalities or sub centers that are adjacent to the principle city or CBD.
Negative exponential function is y=e−x y = e − x . As the the value for x becomes larger, e−x approaches zero.
Bid-rent is a theory that establishes a relationship between price and demand for real estate and distance from city center.
Empirical econometric model is a model that predits the distribution of activities across a number of geographic units (like TAZs or tracts) by the of different activities.
Simultaneous linear regression are a type of statistical models in which dependent variables are functions of other dependent variables, rather than just independent variable
Endogenous s a variable whose measure is determined by the model.
Exogenous is a type of variable that is outside of the model or is imposed on the model.
Expected maximum utility is a rational-based expectations of utility an individual obtains from engaging in an activity.
O-D trip matrix is a matrix in four step travel demand model that shows the flows of trips between each pair of zones.
Friction factors are a function that measures and quantifies the reluctance or impedance of making trips to various duration or distances, which increases in travel distance, time or cost increases.
Three-step least squares is a structure of multivariate regression that defines instrument variables for explaining the dependent variables.
The root-mean-square (RMS) technique is a measure of model prediction accuracy, that is, the more different the model prediction is from the observed data, the larger RMS or model error is.

Key Takeaways

In this chapter, we covered:

How urban form influences travel pattern
Urban forms can be categorized based on their centrality, density, and secondary sub-center development.
Three acknowledged methods exist for quantifying urban form, all of which are derived from the concept of declining bid-rent function.
The appropriate methods for predicting population and employment center growth within metro areas are based on spatial socio-economic characteristics.

Prep/quiz/assessments

What are the different types of urban spatial structures concerning employment agglomeration, and what are their characteristics?
Explain the relationship between different urban structures and the distribution of travel demand for different trip purposes.
What are the three different methods of urban structure quantifications, and what are their main assumptions?
List the primary goals of empirical econometric models and discuss their components and shortcomings.

References

Agarwal, A., Giuliano, G., & Redfearn, C. L. (2012). Strangers in our midst: The usefulness of exploring polycentricity. The Annals of Regional Science, 48(2), 433–450. https://doi.org/10.1007/s00168-012-0497-1

Anas, A. (2013). Modelling in urban and regional economics. Taylor & Francis. https://www.taylorfrancis.com/chapters/mono/10.4324/9781315014791-1/modeling-urban-regional-economics-alex-anas

Anas, A., Arnott, R., & Small, K. A. (1998). Urban spatial structure. Journal of Economic Literature, 36(3), 1426–1464. https://www.jstor.org/stable/2564805

Bertaud, A. (2021). Order without design : how markets shape cities. The Mit Press. https://mitpress.mit.edu/9780262038768/order-without-design/

Boarnet, M. G., Hong, A., & Santiago-Bartolomei, R. (2017). Urban spatial structure, employment subcenters, and freight travel. Journal of Transport Geography, 60, 267–276. https://doi.org/10.1016/j.jtrangeo.2017.03.007

Clark, J. W. (1975). Assessing the relationship between urban form and travel requirements: A literature review and conceptual framework. Depts. of Urban Planning and Civil Engineering, University of Washington.

Gordon, P., Richardson, H. W., & Wong, H. L. (1986). The distribution of population and employment in a polycentric City: The Case of Los Angeles. Environment and Planning A: Economy and Space, 18(2), 161–173. https://doi.org/10.1068/a180161

Hansen, W. (1959). How accessibility shapes land use. Journal of the American Institute of Planners, 25(2), 73–76. https://doi.org/10.1080/01944365908978307

Hill, Donald M., Daniel Brand, and Willard B. Hansen. “Prototype development of statistical land-use prediction model for Greater Boston region.” Highway Research Record 114 (1966).

Néchet, F. L. (2012). Urban spatial structure, daily mobility and energy consumption: a study of 34 European cities. Cybergeo. document 580 https://doi.org/10.4000/cybergeo.24966

Lefèvre, B. (2009). Urban Transport Energy Consumption: Determinants and Strategies for its Reduction.. An analysis of the literature. SAPI EN. S. Surveys and Perspectives Integrating Environment and Society, (2.3).

Pan, Q., Jin, Z., & Liu, X. (2020). Measuring the effects of job competition and matching on employment accessibility. Transportation Research Part D: Transport and Environment, 87, 102535.

Parsons, Brinckerhoff, Quade, & Douglas. (1999). Land use impacts of transportation: A guidebook (Vol. 423). Idaho Transportation Department Reseach Library

Rodrigue, J.-P. (2020). The geography of transport systems. Routledge.

Small, K. A., & Song, S. (1994). Population and employment densities: Structure and change. Journal of Urban Economics, 36(3), 292–313. https://doi.org/10.1006/juec.1994.1037

Stokes, E. (1974). The evaluation of an Empiric model for an urban area. Environment and Planning A, 6(6), 703–715. https://doi.org/10.1068/a060703

Wilson, A. G. (1971). A family of spatial interaction models, and associated developments. Environment and Planning A, 3(1), 1–32. https://doi.org/10.1068/a030001

Zhang, Y., Cheng, T., & Aslam, N. S. (2019). Exploring the relationship between travel pattern and social-demographics using smart card data and household survey. International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, XLII-2/W13, 1375–1382. https://doi.org/10.5194/isprs-archives-xlii-2-w13-1375-2019

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Transportation Land Use Modeling and Policy (TLUMP) Copyright © 2024 by Qisheng Pan and Soheil Sharifi is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.