Glossary

Anurag Pande; Peyton Ratto; Ahmed Farid

Glossary

Chapter 1

Degree[1] – a unit of measure for angles equal to an angle with its vertex at the center of a circle and its sides cutting off ¹/₃₆₀ of the circumference

Law of Cosines[1] – a law in trigonometry: the square of a side of a plane triangle equals the sum of the squares of the remaining sides minus twice the product of those sides and the cosine of the angle between them

Law of Sines[1] – a law in trigonometry: the ratio of each side of a plane triangle to the sine of the opposite angle is the same for all three sides and angles

Radian[1] – a unit of plane angular measurement that is equal to the angle at the center of a circle subtended by an arc whose length equals the radius or approximately 57.3 degrees

Trigonometric Function[1] – a function (such as the sine, cosine, tangent, cotangent, secant, or cosecant) of an arc or angle most simply expressed in terms of the ratios of pairs of sides of a right-angled triangle.

Chapter 2

Binomial[1] – a mathematical expression consisting of two terms connected by a plus sign or minus sign

Common Factor[1] – (also called common divisor) a number or expression that divides two or more numbers or expressions without remainder

Exponent[1] – a symbol written above and to the right of a mathematical expression to indicate the operation of raising to a power

Exponential Function[1] – a mathematical function in which an independent variable appears in one of the exponents

Exponential Growth[2] – a process that increases quantity over time at an ever-increasing rate. It occurs when the instantaneous rate of change (that is, the derivative) of a quantity with respect to time is proportional to the quantity itself.

Logarithm[1] – the exponent that indicates the power to which a base number is raised to produce a given number

Logarithmic Function[1] – a function (such as y =loga x or y = ln x) that is the inverse of an exponential function (such as y = ax or y = ex) so that the independent variable appears in a logarithm

Polynomial[1] – a mathematical expression of one or more algebraic terms each of which consists of a constant multiplied by one or more variables raised to a nonnegative integral power (such as a + bx + cx2)

Chapter 3

Augmented Matrix[1] – a matrix whose elements are the coefficients of a set of simultaneous linear equations with the constant terms of the equations entered in an added column

Matrix[1] – a rectangular array of mathematical elements of simultaneous linear equations that can be combined to form sums and products with similar arrays having an appropriate number of rows and columns

Chapter 4

Derivative[1] – the limit of the ratio of the change in a function to the corresponding change in its independent variable as the latter change approaches zero

Rate of Change[1] – a value that results from dividing the change in a function of a variable by the change in the variable

Slope[1] – the slope of the line tangent to a plane curve at a point

Tangent[1] – meeting a curve or surface in a single point if a sufficiently small interval is considered

Rational Function[1] – a function that is the quotient of two polynomials

Integration[1] – the operation of finding whose differential is known\

Indefinite[1] – having no exact limits

Definite[1] – having distinct or certain limits

Natural Logarithm[1] – a logarithm with e as a base

Absolute Value[1] – a nonnegative number equal in numerical value to a given real number

Piecewise[1] – with respect to a number of discrete intervals, sets, or pieces

Riemann Integral[1] – a definite integral defined as the limit of sums found by partitioning the interval comprising the domain of definition into subintervals, by finding the sum of products each of which consists of the width of a subinterval multiplied by the value of the function at some point in it, and by letting the maximum width of the subintervals approach zero

Fundamental Theorem of Calculus[3] – the theorem, central to the entire development of calculus, that establishes the relationship between differentiation and integration

Fundamental Theorem of Calculus, Part 1[3] – uses a definite integral to define an antiderivative of a function

Fundamental Theorem of Calculus, Part 2[3] – (also, evaluation theorem) we can evaluate a definite integral by evaluating the antiderivative of the integrand at the endpoints of the interval and subtracting

Chapter 5

Acceleration[4] – the rate at which an object’s velocity changes over a period of time

Acceleration due to Gravity[4] – acceleration of an object as result of gravity

Accuracy[4] – the degree to which a measured value agrees with correct value for that measurement

Angular Velocity[4] – 𝜔, the rate of change of the angle with which an object moves on a circular path

Arc Length[4] – ∆𝑠, the distance traveled by an object along a circular path

Average Acceleration[4] – the change in velocity divided by the time over which it changes

Average Speed[4] – distance traveled divided by time during which motion occurs

Average Velocity[4] – displacement divided by the time over which displacement occurs

Banked Curve[4] – the curve in a road that is sloping in a manner that helps a vehicle negotiate the curve

Center of Mass[4] – the point where the entire mass of an object can be thought to be concentrated

Centrifugal Force[4] – a fictitious force that tends to throw an object off when the object is rotating in a non-inertial frame of reference

Centripetal Acceleration[4] – the acceleration of an object moving in a circle, directed toward the center

Centripetal Force[4] – any net force causing uniform circular motion

Classical Physics[4] – physics that was developed from the Renaissance to the end of the 19th century

Conversion Factor[4] – a ratio expressing how many of one unit are equal to another unit

Coriolis Force[4] – the fictitious force causing the apparent deflection of moving objects when viewed in a rotating frame of reference

Deceleration[4] – acceleration in the direction opposite to velocity; acceleration that results in a decrease in velocity

Displacement[4] – the change in position of an object

Distance[4] – the magnitude of displacement between two positions

Distance Traveled[4] – the total length of the path traveled between two positions

Elapsed Time[4] – the difference between the ending time and beginning time

English Units[4] – system of measurement used in the United States; includes units of measurement such as feet, gallons, and pounds

External Force[4] – a force acting on an object or system that originates outside of the object or system

Fictious Force[4] – a force having no physical origin

Force[4] – a push or pull on an object with a specific magnitude and direction; can be represented by vectors; can be expressed as a multiple of a standard force

Free-body Diagram[4] – a sketch showing all of the external forces acting on an object or system; the system is represented by a dot, and the forces are represented by vectors extending outward from the dot

Free-Fall[4] – a situation in which the only force acting on an object is the force due to gravity

Friction[4] – a force past each other of objects that are touching; examples include rough surfaces and air resistance

Gravitational Constant, G[4] – a proportionality factor used in the equation for Newton’s universal law of gravitation; it is a universal constant—that is, it is thought to be the same everywhere in the universe

Ideal Banking[4] – the sloping of a curve in a road, where the angle of the slope allows the vehicle to negotiate the curve at a certain speed without the aid of friction between the tires and the road; the net external force on the vehicle equals the horizontal centripetal force in the absence of friction

Ideal Speed[4] – the maximum safe speed at which a vehicle can turn on a curve without the aid of friction between the tire and the road

Inertia[4] – the tendency of an object to remain at rest or remain in motion

Inertial Frame of Reference[4] – a coordinate system that is not accelerating; all forces acting in an inertial frame of reference are real forces, as opposed to fictitious forces that are observed due to an accelerating frame of reference

Instantaneous Acceleration[4] – acceleration at a specific point in time

Instantaneous Speed[4] – magnitude of the instantaneous velocity

Instantaneous Velocity[4] – velocity at a specific instant, or the average velocity over an infinitesimal time interval

Kilogram[4] – the SI unit for mass, abbreviated (kg)

Kinematics[4] – the study of motion without considering its causes

Kinetic Friction[4] – a force that opposes the motion of two systems that are in contact and moving relative to one another

Law[4] – a description, using concise language or a mathematical formula, a generalized pattern in nature that is supported by scientific evidence and repeated experiments

Law of Inertia[4] – see Newton’s first law of motion

Magnitude of Kinetic Friction[4] – 𝑓𝑘=𝜇_𝑘𝑁, where 𝜇_𝑘is the coefficient of kinetic friction

Magnitude of Static Friction[4] – 𝑓_𝑠≤𝜇_𝑠𝑁, where 𝜇_𝑠is the coefficient of static friction and 𝑁 is the magnitude of the normal force

Mass[4] – the quantity of matter in a substance; measured in kilograms

Meter[4] – the SI unit for length, abbreviated (m)

Metric System[4] – a system in which values can be calculated in factors of 10

Model[4] – simplified description that contains only those elements necessary to describe the physics of a physical situation

Net External Force[4] – the vector sum of all external forces acting on an object or system; causes a mass to accelerate

Newton’s First Law of Motion[4] – in an inertial frame of reference, a body at rest remains at rest, or, if in motion, remains in motion at a constant velocity unless acted on by a net external force; also known as the law of inertia

Newton’s Second Law of Motion[4] – the net external force 𝐹_𝑛𝑒𝑡on an object with mass 𝑚 is proportional to and in the same direction as the acceleration of the object, 𝑎, and inversely proportional to the mass; defined mathematically as $a=\frac{F_{n e t}}{m}$

Newton’s Third Law of Motion[4] – whenever one body exerts a force on a second body, the first body experiences a force that is equal in magnitude and opposite in direction to the force that the first body exerts

Newton’s Universal Law of Gravitation[4] – every particle in the universe attracts every other particle with a force along a line joining them; the force is directly proportional to the product of their masses and inversely proportional to the square of the distance between them

Non-Inertial Frame of Reference[4] – an accelerated frame of reference

Normal Force[4] – the force that a surface applies to an object to support the weight of the object; acts perpendicular to the surface on which the object rests

Physical Quantity[4] – a characteristic or property of an object that can be measured or calculated from other measurements

Physics[4] – the science concerned with describing the interactions of energy, matter, space, and time; it is especially interested in what fundamental mechanisms underlie every phenomenon

Pit[4] – a tiny indentation on the spiral track moulded into the top of the polycarbonate layer of CD

Position[4] – the location of an object at a particular time

Radians[4] – a unit of angle measurement

Radius of Curvature[4] – radius of a circular path

Rotation Angle[4] – the ratio of arc length to the radius of curvature on a circular path: $\Delta \theta=\frac{\Delta s}{r}$

Scalar[4] – a quantity that is described by magnitude, but not direction

Second[4] – the SI unit for time, abbreviated (s)

SI Units[4] – the international system of units that scientists in most countries have agreed to use; includes units such as meters, liters, and grams

Significant Figures[4] – express the precision of a measuring tool used to measure a value

Slope[4] – the difference in y-value (the rise) divided by the difference in x-value (the run) of two points on a straight line

Static Friction[4] – a force that opposes the motion of two systems that are in contact and are not moving relative to one another

System[4] – defined by the boundaries of an object or collection of objects being observed; all forces originating from outside of the system are considered external forces

Tension[4] – the pulling force that acts along a medium, especially a stretched flexible connector, such as a rope or cable; when a rope supports the weight of an object, the force on the object due to the rope is called a tension force

Thrust[4] – a reaction force that pushes a body forward in response to a backward force; rockets, airplanes, and cars are pushed forward by a thrust reaction force

Time[4] – change, or the interval over which change occurs

Ultracentrifuge[4] – a centrifuge optimized for spinning a rotor at very high speeds

Uniform Circular Motion[4] – the motion of an object in a circular path at constant speed

Units[4] – a standard used for expressing and comparing measurements

Vector[4] – a quantity that is described by both magnitude and direction

Weight[4] – the force 𝑤 due to gravity acting on an object of mass 𝑚; defined mathematically as: 𝑤=𝑚𝑔, where 𝑔 is the magnitude and direction of the acceleration due to gravity

Y-Intercept[4] – the y-value when 𝑥=0, or when the graph crosses the y-axis

Chapter 6

Center of Gravity[4] – the point where the total weight of the body is assumed to be concentrated

Change in Momentum[4] – the difference between the final and initial momentum; the mass times the change in velocity

Conservation of Momentum Principle[4] – when the net external force is zero, the total momentum of the system is conserved or constant

Dynamic Equilibrium[4] – a state of equilibrium in which the net external force and torque on a system moving with constant velocity are zero

Elastic Collision[4] – a collision that also conserves internal kinetic energy

Impulse[4] – the average net external force times the time it acts; equal to the change in momentum

Inelastic Collision[4] – a collision in which internal kinetic energy is not conserved

Internal Kinetic Energy[4] – the sum of the kinetic energies of the objects in a system

Isolated System[4] – a system in which the net external force is zero

Linear Momentum[4] – the product of mass and velocity

Neutral Equilibrium[4] – a state of equilibrium that is independent of a system’s displacements from its original position

Perfectly Inelastic Collision[4] – a collision in which the colliding objects stick together

Perpendicular Lever Arm[4] – the shortest distance from the pivot point to the line along which 𝐹 lies

Point Masses[4] – structureless particles with no rotation or spin

Second Law of Motion[4] – physical law that states that the net external force equals the change in momentum of a system divided by the time over which it changes

SI Units of Torque[4] – newton times meters, usually written as 𝑁∙𝑚

Stable Equilibrium[4] – a system, when displaced, experiences a net force or torque in a direction opposite to the direction of the displacement

Static Equilibrium[4] – a state of equilibrium in which the net external force and torque acting on a system is zero; equilibrium in which the acceleration of the system is zero and accelerated rotation does not occur

Torque[4] – turning or twisting effectiveness of a force

Unstable Equilibrium[4] – a system, when displaced, experiences a net force or torque in the same direction as the displacement from equilibrium

Chapter 7

Amplitude[4] – the maximum displacement from the equilibrium position of an object oscillating around the equilibrium position

Doppler effect[4] – an alteration in the observed frequency of a sound due to motion of either the source or the observer

Doppler shift[4] – the actual change in frequency due to relative motion of source and observer

Frequency[4] – number of events per unit of time

Hearing[4] – the perception of sound

Intensity[4] – power per unit area; sounds below 20 Hz

Longitudinal Wave[4] – a wave in which the disturbance is parallel to the direction of propagation

Loudness[4] – the perception of sound intensity

Natural Frequency[4] – the frequency at which a system would oscillate if there were no driving and no damping forces

Period[4] – time it takes to complete one oscillation

Pitch[4] – the perception of the frequency of a sound

Sound[4] – a disturbance of matter that is transmitted from its source outward

Sound Intensity Level[4] – a unitless quantity telling you the level of the sound relative to a fixed standard

Sound Pressure Level[4] – the ratio of the pressure amplitude to a reference pressure

Tone[4] – number and relative intensity of multiple sound frequencies

Traverse Wave[4] – a wave in which the disturbance is perpendicular to the direction of propagation

Wave[4] – a disturbance that moves from its source and carries energy

Wave Velocity[4] – the speed at which the disturbance moves. Also called the propagation velocity or propagation speed

Wavelength[4] – the distance between adjacent identical parts of a wave

Chapter 8

Bayes Theorem[6] – a useful tool for calculating conditional probability. Bayes theorem can be expressed as: 𝐴₁, 𝐴₂,…, 𝐴_𝑛be a set of mutually exclusive events that together form the sample space S. Let B be any event from the same sample space, such that 𝑃(𝐵)>0. Then, $P(A \mid B)=\frac{P(A) P(B \mid A)}{P(B)}$

Bernoulli Trials[5] – an experiment with the following characteristics: (1) There are only two possible outcomes called “success” and “failure” for each trial. (2) The probability p of a success is the same for any trial (so the probability 𝑞=1−𝑝 of a failure is the same for any trial).

Binomial Experiment[5] – a statistical experiment that satisfies the following three conditions: (1) There are a fixed number of trials, n. (2) There are only two possible outcomes, called “success” and, “failure,” for each trial. The letter p denotes the probability of a success on one trial, and q denotes, the probability of a failure on one trial. (3) The n trials are independent and are repeated using identical conditions.

Binomial Probability Distribution[5] – a discrete random variable that arises from Bernoulli trials; there are a fixed number, n, of independent trials. “Independent” means that the result of any trial (for example, trial one) does not affect the results of the following trials, and all trials are conducted under the same conditions. Under these circumstances the binomial random variable X is defined as the number of successes in n trials. The mean is 𝜇=𝑛𝑝 and the standard deviation is $\sigma=\sqrt{n p q} .$ The probability of exactly x successes in n trials is $P(X=x)=\left(\begin{array}{l} n \\ x \end{array}\right) p^x q^{n-x}$

Combination[6] – a combination is a selection of all or part of a set of objects, without regard to the order in which objects are selected

Conditional Probability[5] – the likelihood that an event will occur given that another event has already occurred.

Discrete Variable / continuous variable[6] – if a variable can take on any value between its minimum value and its maximum value, it is called a continuous variable; otherwise it is called a discrete variable

Expected Value[6] – the mean of the discrete random variable X is also called the expected value of X. Notationally, the expected value of X is denoted by 𝐸(𝑋).

Exponential Distribution[5] – a continuous random variable that appears when we are interested in the intervals of time between some random events, for example, the length of time between emergency arrivals at a hospital. The mean is $\mu=\frac{1}{m}$ and the standard deviation is $\sigma=\frac{1}{m}$ . The probability density function is $f(x)=\frac{1}{\mu} e^{\left(-\frac{1}{\mu}\right) x}, x \geq 0 \text { and the cumulative distribution function is } P(X \leq x)=1-e^{\left(-\frac{1}{\mu}\right) x}$

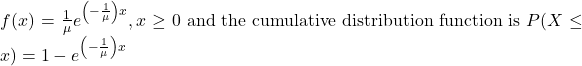
Geometric Distribution[5] – a discrete random variable that arises from the Bernoulli trials; the trials are repeated until the first success. The geometric variable X is defined as the number of trials until the first success. The mean is $\mu=\frac{1}{p} \text { and the standard deviation is } \sigma=\sqrt{\frac{1}{p}\left(\frac{1}{p}-1\right)} \text {. }$ The probability of exactly x failures before the first success is given by the formula: 𝑃(𝑋=𝑥)=𝑝(1−𝑝)^𝑥−1where one wants to know probability for the number of trials until the first success: the xth trial is the first success. An alternative formulation of the geometric distribution asks the question: what is the probability of x failures until the first success? In this formulation the trial that resulted in the first success is not counted. The formula for this presentation of the geometric is: 𝑃(𝑋=𝑥)=𝑝(1−𝑝)^𝑥. The expected value in this form of the geometric distribution is $\mu=\frac{1-p}{p}$ . The easiest way to keep these two forms of the geometric distribution straight is to remember that p is the probability of success and (1−𝑝) is the probability of failure. In the formula the exponents simply count the number of successes and number of failures of the desired outcome of the experiment. Of course the sum of these two numbers must add to the number of trials in the experiment.

Geometric Experiment[5] – a statistical experiment with the following properties: (1) There are one or more Bernoulli trials with all failures except the last one, which is a success. (2) In theory, the number of trials could go on forever. There must be at least one trial. (3) The probability, p, of a success and the probability, q, of a failure do not change from trial to trial.

Independent[6] – two events are independent when the occurrence of one does not affect the probability of the occurrence of the other

Mean[6] – a mean score is an average score, often denoted by $\bar{X}$ . It is the sum of individual scores divided by the number of individuals.

Memoryless Property[5] – For an exponential random variable X, the memoryless property is the statement that knowledge of what has occurred in the past has no effect on future probabilities. This means that the probability that X exceeds 𝑥+𝑡, given that it has exceeded x, is the same as the probability that X would exceed t if we had no knowledge about it. In symbols we say that $P(X>x+t \mid X>x)=P(X>t)$ .

Multiplication Rule[6] – If events A and B come from the same sample space, the probability that both A and B occur is equal to the probability the event A occurs time the probability that B occurs, given that A has occurred. $P(A \cap B)=P(A) P(B \mid A)$ .

Normal Distribution[5] – a continuous random variable with pdf $f(x)=\frac{1}{\sigma \sqrt{2 \pi}} e^{\frac{-(x-\mu)^2}{2 \sigma^2}}$ , where 𝜇 is the mean of the distribution and 𝜎 is the standard deviation; notation: $X \sim N(\mu, \sigma) \text {. If } \mu=0 \text { and } \sigma=1 \text {, }$ , the random variable, Z, is called the standard normal distribution

Permutation[6] – an arrangement of all or part of a set of objects, with regard to the order of the arrangement.

Poisson Distribution[5] – If there is a known average of 𝜇 events occurring per unit time, and these events are independent of each other, then the number of events X occurring in one unit of time has the Poisson distribution. The probability of x events occurring in one unit time is equal to $P(X=x)=\frac{\mu^x e^{-\mu}}{x !}$

Poisson Probability Distribution[5] – a discrete random variable that counts the number of times a certain event will occur in a specific interval; characteristics of the variable: (1) the probability that the event occurs in a given interval is the same for all intervals. (2) the events occur with a known mean and independently of the time since the last event. The distribution is defined by the mean 𝜇 of the event in the interval. The mean is 𝜇=𝑛𝑝. The standard deviation is $\sigma=\sqrt{\mu}$ . The probability of having exactly x successes in r trials is $P(x)=\frac{\mu^x e^{-\mu}}{x !}$ . The Poisson distribution is often used to approximate the binomial distribution, when n is “large” and p is “small” (a general rule is that np should be greater than or equal to 25 and p should be less than or equal to 0.01).

Probability Distribution Function (PDF)[5] – a mathematical description of a discrete random variable, given either in the form of an equation (formula) or in the form of a table listing all the possible outcomes of an experiment and the probability associated with each outcome.

Quartile[6] – Quartiles divide a rank-ordered data set into four equal parts. The values that divide each part are called the first, second, and third quartiles; and they are denoted by

𝑄₁, 𝑄₂, and 𝑄₃, respectively.

Random Variable[5] – a characteristic of interest in a population being studied; common notation for variables are upper case Latin letters X, Y, Z..; common notation for a specific value from the domain (set of all possible values of a variable) are lower case Latin letters x, y, and z. For example, if X is the number of children in a family, then x represents a specific integer 0, 1, 2, 3,… Variables in statistics differ from variables in intermediate algebra in the two following ways: (1) The domain of the random variable is not necessarily a numerical set; the domain may be expressed in words; for example, if X = hair color then domain is {black, blonde, gray, green, orange}. (2) We can tell what specific value x the random variable X takes only after performing the experiment.

Standard Deviation[6] – The standard deviation is a numerical value used to indicate how widely individuals in a group vary. If individual observations vary greatly from the group mean, the standard deviation is big; and vice versa. It is important to distinguish between the standard deviation of a population and the standard deviation of a sample. They have different notation, and they are computed differently. The standard deviation of a population is denoted by 𝜎 and the standard deviation of a sample, by 𝑠

Standard Normal Distribution[5] – a continuous random variable 𝑋~𝑁(0,1); when X follows the standard normal distribution, it is often noted as 𝑍~𝑁(0,1).

Uniform Distribution[5] – a continuous random variable that has equally likely outcomes over the domain, 𝑎<𝑥<𝑏; it is often referred as the rectangular distribution because the graph of the pdf has the form of a rectangle. The mean is $\mu=\frac{a+b}{2}$ and the standard deviation is $\sigma=\sqrt{\frac{(b-a)^2}{12}}$ The probability density function is $f(x)=\frac{1}{b-a} \text { for } a<x. The cumulative distribution is [latex]P(X \leq x)=$ $\frac{x-a}{b-a}$

Variance[6] – the variance is a numerical value used to indicate how widely individuals in a group vary. If individual observations vary greatly from the group mean, the variance is big; and vice versa. It is important to distinguish between the variance of a population and the variance of a sample. They have different notation, and they are computed differently. The variance of a population is denoted by 𝜎²; and the variance of a sample, by 𝑠²

Z-Score[5] – the linear transformation of the form $z=\frac{x-\mu}{\sigma} \text { or written as } z=\frac{|x-\mu|}{\sigma}$ ; if this transformation is applied to any normal distribution 𝑋~𝑁(𝜇,𝜎) the result is the standard normal distribution 𝑍~𝑁(0,1). If this transformation is applied to any specific value x of the random variable with mean 𝜇 and standard deviation 𝜎, the result is called the z-score of x. The z-score allows us to compare data that are normally distributed but scaled differently. A z-score is the number of standard deviations a particular x is away from its mean value.

Chapter 9

𝑹^𝟐– Coefficient of Determination[5] – this is a number between 0 and 1 that represents the percentage variation of the dependent variable that can be explained by the variation in the independent variable. Sometimes calculated by the equation $R^2=\frac{S S R}{S S T}$ where SSR is the “sum of squares regressions” and SST is the “sum of squares total.” The appropriate coefficient of determination to be reported should always be adjusted for degrees of freedom first

A is the Symbol for the y-Intercept[5] – sometimes written as 𝑏₀, because when writing the theoretical linear model 𝛽₀is used to represent a coefficient for a population

Analysis of Variance[5] – also referred to as ANOVA, is a method of testing whether or not the means of three or more populations are equal. The method is applicable if: (1) all populations of interest are normally distributed (2) the populations have equal standard deviations (3) samples (not necessarily of the same size) are randomly and independently selected from each population (4) there is one independent variable and one dependent variable. The test statistic for analysis of variance is the F-ratio

Average[5] – a number that describes the central tendency of the data; there are a number of specialized averages, including the arithmetic mean, weighted mean, median, mode, and geometric mean.

B is the Symbol for Slope[5] – the word coefficient will be used regularly for the slope, because it is a number that will always be next to the letter “x.” It will be written a 𝑏₁when a sample is used, and 𝛽₁will be used with a population or when writing the theoretical linear model.

Binomial Distribution[5] – a discrete random variable which arises from Bernoulli trials; there are a fixed number, n, of independent trials. “Independent” means that the result of any trial (for example, trial 1) does not affect the results of the following trials, and all trials are conducted under the same conditions. Under these circumstances the binomial random variable X is defined as the number of successes in n trials. The notation is: 𝑋~𝐵(𝑛,𝑝). The mean is 𝜇=𝑛𝑝 and the standard deviation is $\sigma=\sqrt{n p q}$ . The probability of exactly x successes in n trials is $P(X=x)=\left(\begin{array}{l} n \\ x \end{array}\right) p^x q^{n-x}$

Bivariate[5] – two variables are present in the model where one is the “cause” or independent variable and the other is the “effect” of dependent variable.

Central Limit Theorem[5] – given a random variable with known mean 𝜇 and known standard deviation, 𝜎, we are sampling with size n, and we are interested in two new random variables: the sample mean, $\bar{X}$ . If the size (n) of the sample is sufficiently large, then $\bar{X} \sim N\left(\mu, \frac{\sigma}{\sqrt{n}}\right)$ . If the size (n) of the sample is sufficiently large, then the distribution of the sample means will approximate a normal distributions regardless of the shape of the population. The mean of the sample means will equal the population mean. The standard deviation of the distribution of the sample means, $\frac{\sigma}{\sqrt{n}}$ , is called the standard error of the mean.

Cohen’s d [5] – a measure of effect size based on the differences between two means. If d is between 0 and 0.2 then the effect is small. If d approaches is 0.5, then the effect is medium, and if d approaches 0.8, then it is a large effect.

Confidence Interval (CI)[5] – an interval estimate for an unknown population parameter. This depends on: (1) the desired confidence level (2) information that is known about the distribution (for example, known standard deviation) (3) the sample and its size

Confidence Level (CL)[5] – the percent expression for the probability that the confidence interval contains the true population parameter; for example, if the CL = 90%, then in 90 out of 100 samples the interval estimate will enclose the true population parameter.

Contingency Table[5] – a table that displays sample values for two different factors that may be dependent or contingent on one another; it facilitates determining conditional probabilities.

Critical Value[5] – The t or Z value set by the researcher that measures the probability of a Type I error, 𝛼

Degrees of Freedom (df)[5] – the number of objects in a sample that are free to vary

Error Bound for a Population Mean (EBM)[5] – the margin of error; depends on the confidence level, sample size, and known or estimated population standard deviation.

Error Bound for a Population Proportion (EBP)[5] – the margin of error; depends on the confidence level, the sample size, and the estimated (from the sample) proportion of successes.

Goodness-of-Fit[5] – a hypothesis test that compares expected and observed values in order to look for significant differences within one non-parametric variable. The degrees of freedom used equals the (number of categories – 1).

Hypothesis[5] – a statement about the value of a population parameter, in case of two hypotheses, the statement assumed to be true is called the null hypothesis (notation 𝐻₀) and the contradictory statement is called the alternative hypothesis (notation 𝐻_𝑎)

Hypothesis Testing[5] – Based on sample evidence, a procedure for determining whether the hypothesis stated is a reasonable statement and should not be rejected, or is unreasonable and should be rejected.

Independent Groups[5] – two samples that are selected from two populations, and the values from one population are not related in any way to the values from the other population.

Inferential Statistics[5] – also called statistical inference or inductive statistics; this facet of statistics deals with estimating a population parameter based on a sample statistic. For example, if four out of the 100 calculators sampled are defective we might infer that four percent of the production is defective.

Linear[5] – a model that takes data and regresses it into a straight line equation.

Matched Pairs[5] – two samples that are dependent. Differences between a before and after scenario are tested by testing one population mean of differences.

Mean[5] – a number that measures the central tendency; a common name for mean is “average.” The term “mean” is a shortened form of “arithmetic mean.” By definition, the mean for a sample (denoted by $\bar{x}) \text { is } \bar{x}=\frac{\text { sum of all values in the sample }}{\text { number of values in the sample }}$ , and the mean for a population (denoted by 𝜇) is $\frac{\text { sum of all values in the population }}{\text { number of values in the population }}$

Multivariate[5] – a system or model where more than one independent variable is being used to predict an outcome. There can only ever be one dependent variable, but there is no limit to the number of independent variables.

Normal Distribution[5] – a continuous random variable with pdf $f(x)=\frac{1}{\sigma \sqrt{2 \pi}} e^{\frac{-(x-\mu)^2}{2 \sigma^2}}$ , where 𝜇 is the mean of the distribution and 𝜎 is the standard deviation; notation: 𝑋~𝑁(𝜇,𝜎). If 𝜇=0 and 𝜎=1, the random variable, Z, is called the standard normal distribution.

Normal Distribution[5] – a continuous random variable with pdf $f(x)=\frac{1}{\sigma \sqrt{2 \pi}} e^{-(x-\mu)^2 / 2 \sigma^2}$ , where 𝜇 is the mean of the distribution and 𝜎 is the standard deviation, notation:

𝑋~𝑁(𝜇,𝜎) and 𝜎=1, the random variable is called the standard normal distribution.

One-Way ANOVA[5] – a method of testing whether or not the means of three or more populations are equal; the method is applicable if: (1) all populations of interest are normally distributed (2) the populations have equal standard deviations (3) samples (not necessarily of the same size) are randomly and independently selected from each population. The test statistic for analysis of variance is the F-ratio

Parameter[5] – a numerical characteristic of a population

Point Estimate[5] – a single number computed from a sample and used to estimate a population parameter

Pooled Variance[5] – a weighted average of two variances that can then be used when calculating standard error.

R – Correlation Coefficient[5] – A number between −1 and 1 that represents the strength and direction of the relationship between “X” and “Y.” The value for “r” will equal 1 or −1 only if all the plotted points form a perfectly straight line.

Residual or “Error”[5] – the value calculated from subtracting $y_0-\hat{y}_0=e_0$ . The absolute value of a residual measures the vertical distance between the actual value of y and the estimated value of y that appears on the best-fit line.

Sampling Distribution[5] – Given simple random samples of size n from a given population with a measured characteristic such as mean, proportion, or standard deviation for each sample, the probability distribution of all the measured characteristics is called a sampling distribution.

Standard Deviation[5] – a number that is equal to the square root of the variance and measures how far data values are from their mean; notation: s for sample standard deviation and 𝜎 for population standard deviation

Standard Error of the Mean[5] -the standard deviation of the distribution of the sample means, or $\frac{\sigma}{\sqrt{n}}$

Standard Error of the Proportion[5] -the standard deviation of the sampling distribution of proportions

Student’s t-Distribution[5] – investigated and reported by William S. Gossett in 1908 and published under the pseudonym Student; the major characteristics of this random variable are: (1) it is continuous and assumes any real values (2) the pdf is symmetrical about its mean of zero (3) it approaches the standard normal distribution as n gets larger (4) there is a “family” of t-distributions: each representative of the family is completely defined by the number of degrees of freedom, which depends upon the application for which the t is being used.

Sum of Squared Errors (SSE)[5] – the calculated value from adding up all the squared residual terms. The hope is that this value is very small when creating a model.

Test for Homogeneity[5] – a test used to draw a conclusion about whether two populations have the same distribution. The degrees of freedom used equals the (number of columns – 1).

Test of Independence[5] – a hypothesis test that compares expected and observed values for contingency tables in order to test for independence between two variables. The degrees of freedom used equals the (number of columns – 1) multiplied by the (number of rows – 1).

Test Statistic[5] – The formula that counts the number of standard deviations on the relevant distribution that estimated parameter is away from the hypothesized value.

Type I Error[5] -The decision is to reject the null hypothesis when, in fact, the null hypothesis is true.

Type II Error[5] – The decision is not to reject the null hypothesis when, in fact, the null hypothesis is false.

Variance[5] – mean of the squared deviations from the mean; the square of the standard deviation. For a set of data, a deviation can be represented as $x-\bar{x}$ where x is a value of the data and $\bar{x}$ is the sample mean. The sample variance is equal to the sum of the squares of the deviations divided by the difference of the sample size and one.

X – the Independent Variable[5] – This will sometimes be referred to as the “predictor” variable, because these values were measured in order to determine what possible outcomes could be predicted.

Y – the Dependent Variable[5] – also, using the letter “y” represents actual values while $\hat{y}$ represents predicted or estimated values. Predicted values will come from plugging in observed “x” values into a linear model

Glossary references

[1] Merriam-Webster.com. Retrieved July 6, 2023, from https://www.merriam-webster.com/

[2] Wikipedia.com. Retrieved January 16, 2024, from https://en.wikipedia.org/wiki/Exponential_growth

[3] “Calculus Volume 1” by Gilbert Strang, Edwin “Jed” Herman on OpenStax, Chapter 5.3: The Fundamental Theorem of Calculus https://openstax.org/books/calculus-volume-1/pages/5-3-the-fundamental-theorem-of-calculus

[4] “College Physics for AP® Courses” by Greg Wolfe, Erika Gasper, John Stoke, Julie Kretchman, David Anderson, Nathan Czuba, Sudhi Oberoi, Liza Pujji, Irina Lyublinskaya, Douglas Ingram. Access for free at https://openstax.org/books/college-physics-ap-courses/pages/1-connection-for-ap-r-courses

[5] “Introductory Business Statistics” by Alexander Holmes, Barbara Illowsky, and Susan Dean on OpenStax. Access for free at https://openstax.org/books/introductory-business-statistics/pages/1-introduction

[6] Berman H.B., “Statistics Dictionary”, [online] Available at: https://stattrek.com/statistics/dictionary?definition=select-term URL [Accessed Date: 8/16/2022].

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Fundamentals of Math, Physics, and Statistics for Future Transportation Professionals Copyright © 2024 by Anurag Pande; Peyton Ratto; and Ahmed Farid is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.