Chapter 1: Trigonometry Functions and Geometric Measurements
This chapter will discuss the basic geometric and trigonometric functions and measurements because they are important in transportation engineering for the functional design of facilities, including roadways, railroads, and intersection sight distance.
Learning Objectives
At the end of the chapter, the reader should be able to do the following:
- Recognize, rearrange, and simplify trigonometric functions.
- Apply properties of triangles to solve for sides and angles.
- Identify transportation engineering topics where the properties of triangles and trigonometric functions are used.
- Identify topics in the introductory transportation engineering courses that build on the concepts discussed in this chapter.
Recognize, Rearrange, and Simplify Trigonometric Functions
This section will explain basic manipulation of trigonometric functions with videos to help your comprehension. Also, short problems to check your understanding are included.
Radians & Degrees
Check Your Understanding: Radians & Degrees
Solving Similar Triangles
Check Your Understanding: Solving Similar Triangles
Introduction to the Trigonometric Ratios
Check Your Understanding: Introduction to the Trigonometric Ratios
The Trig Functions & Right Triangle Trig Ratios
Check Your Understanding: The Trig Functions & Right Triangle Trig Ratios
Solving for a Side in a Right Triangle Using the Trigonometric Ratios
Check Your Understanding: Solving for a Side in a Right Triangle Using the Trigonometric Ratios
The Inverse Trigonometric Functions
Introduction to Arcsine
Introduction to Arctangent
Introduction to Arccosine
Check Your Understanding: The Inverse Trigonometric Functions
Law of Sines
Check Your Understanding: Law of Sines
Law of Cosines
Check Your Understanding: Law of Cosines
Check Your Understanding: Recognize, Rearrange, and Simplify Trigonometric Functions Overall
Identify Properties for Circular, Parabolic, and Spiral Curves
This section uses videos to understand the elements of simple circular curves, parabolic curves, and spiral curves.
Elements of Simple Circular Curves
Elements of Parabolic Curves
Elements of Spiral Curves
Relevance to Transportation Engineering Coursework
This section will explain horizontal straight road sections, curves, and spiral transition sections that connect them.
Horizontal Profile
Transportation engineers apply the trigonometric functions discussed here in the process of designing roads, and in particular, their horizontal profiles. The horizontal profile describes the horizontal straight road sections, curves, and spiral transition sections (see Figure 1) that connect them. The curves’ geometric design elements depend on principles discussed in the following sections of this chapter: “Radians & Degrees”, “Solving Similar Triangles”, “Introduction to the Trigonometric Ratios”, “The Trig Functions & Right Triangle Trig Ratios”, “Solving for a Side in a Right Triangle Using the Trigonometric Ratios”, and “The Inverse Trigonometric Functions”. For details of the design process (discussed in the Fundamentals of Transportation Engineering course) please review the above section titled “Elements of Simple Circular Curves”.

Stopping Sight Distance on Horizontal Curves
The stopping sight distance (SSD) is the minimum distance a driver needs to perceive an unusual situation, such as a deer crossing the road, and stop to avoid a collision. Along horizontal curves, the driver’s line of sight may be obstructed by trees or other roadside objects (see Figure 2). The formula for computing the minimum required SSD on horizontal curves near sight obstructions is derived using the principles discussed in the following sections: “Radians & Degrees”, “Solving Similar Triangles”, “Introduction to the Trigonometric Ratios”, “The Trig Functions & Right Triangle Trig Ratios”, “Solving for a Side in a Right Triangle Using the Trigonometric Ratios”, and “The Inverse Trigonometric Functions”.

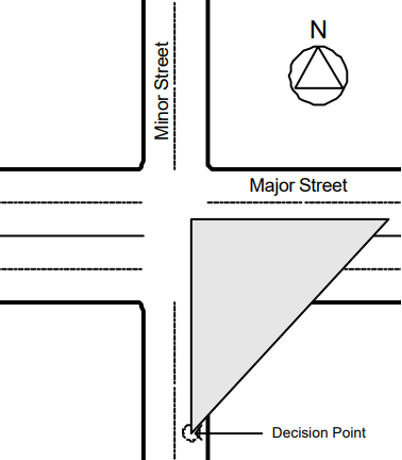
Sight Triangles at Intersections
When approaching an intersection, drivers should be able to see it from a distance to be able to stop in time before colliding with other approaching vehicles, pedestrians, and bicyclists. This distance is computed by first constructing “sight triangles” similar to the one shown in Figure 3. The sight triangle computations are made using the principle of similar triangles (see the section titled “Solving Similar Triangles” above).
Key Takeaways
- Transportation engineers apply trigonometric functions to design roads and railroad tracks, particularly their horizontal profiles. Knowledge of these functions is critical to ensuring that on segments with horizontal curvature (or bend around the corner), road users have adequate sight distance available to negotiate the curve on the travel way safely.
- The knowledge of trigonometry is also critical to solving intersection sight triangles and estimating Intersection Sight Distance (ISD) required to safely navigate the intersections.
Glossary: Key Terms
Degree[1] – a unit of measure for angles equal to an angle with its vertex at the center of a circle and its sides cutting off ¹/₃₆₀ of the circumference
Law of Cosines[1] – a law in trigonometry: the square of a side of a plane triangle equals the sum of the squares of the remaining sides minus twice the product of those sides and the cosine of the angle between them
Law of Sines[1] – a law in trigonometry: the ratio of each side of a plane triangle to the sine of the opposite angle is the same for all three sides and angles
Radian[1] – a unit of plane angular measurement that is equal to the angle at the center of a circle subtended by an arc whose length equals the radius or approximately 57.3 degrees
Trigonometric Function[1] – a function (such as the sine, cosine, tangent, cotangent, secant, or cosecant) of an arc or angle most simply expressed in terms of the ratios of pairs of sides of a right-angled triangle.
Media Attributions
Note: All Khan Academy content is available for free at (www.khanacademy.org).
Videos
- Video 1: Radians & Degrees by Khan Academy is licensed by Creative Commons NonCommercial-ShareAlike 3.0 United States (CC BY-NC-SA 3.0 US)
- Video 2: Solving Similar Triangles by Khan Academy is licensed by Creative Commons NonCommercial-ShareAlike 3.0 United States (CC BY-NC-SA 3.0 US)
- Video 3: Introduction to the Trigonometric Ratios by Khan Academy is licensed by Creative Commons NonCommercial-ShareAlike 3.0 United States (CC BY-NC-SA 3.0 US)
- Video 4: The Trig Functions & Right Triangle Trig Ratios by Khan Academy is licensed by Creative Commons NonCommercial-ShareAlike 3.0 United States (CC BY-NC-SA 3.0 US)
- Video 5: Solving for a Side in a Right Triangle Using the Trigonometric Ratios by Khan Academy is licensed by Creative Commons NonCommercial-ShareAlike 3.0 United States (CC BY-NC-SA 3.0 US)
- Video 6: Introduction to arcsine by Khan Academy is licensed by Creative Commons NonCommercial-ShareAlike 3.0 United States (CC BY-NC-SA 3.0 US)
- Video 7: Introduction to arctangent by Khan Academy is licensed by Creative Commons NonCommercial-ShareAlike 3.0 United States (CC BY-NC-SA 3.0 US)
- Video 8: Introduction to arccosine by Khan Academy is licensed by Creative Commons NonCommercial-ShareAlike 3.0 United States (CC BY-NC-SA 3.0 US)
- Video 9: Law of Sines by Khan Academy is licensed by Creative Commons NonCommercial-ShareAlike 3.0 United States (CC BY-NC-SA 3.0 US)
- Video 10: Law of Cosines by Khan Academy is licensed by Creative Commons NonCommercial-ShareAlike 3.0 United States (CC BY-NC-SA 3.0 US)
- Video 11: Elements of Simple Circular Curves by Mr. Shashikant B. Gosavi, Assistant Professor, Department of Civil Engineering, Walchand Institute of Technology, Solapur is licensed by Attribution 3.0 Unported (CC BY 3.0)
- Video 12: Elements of Parabolic Curves by Mr. Ashok Kumar, Assistant Professor, Department of Civil Engineering, Walchand Institute of Technology, Solapur is licensed by Attribution 3.0 Unported (CC BY 3.0)
- Video 13: Elements of Spiral Curves by Mr. Ashok Kumar, Assistant Professor, Department of Civil Engineering, Walchand Institute of Technology, Solapur is licensed by Attribution 3.0 Unported (CC BY 3.0)
Figures
References
- Farid, A. (2022). Highway Design. Personal Collection of Ahmed Farid, California Polytechnic State University, San Luis Obispo, CA.
- Farid, A. (2022). Considerations for Intersections. Personal Collection of Ahmed Farid, California Polytechnic State University, San Luis Obispo, CA.
a function (such as the sine, cosine, tangent, cotangent, secant, or cosecant) of an arc or angle most simply expressed in terms of the ratios of pairs of sides of a right-angled triangle.
a unit of plane angular measurement that is equal to the angle at the center of a circle subtended by an arc whose length equals the radius or approximately 57.3 degrees
a unit of measure for angles equal to an angle with its vertex at the center of a circle and its sides cutting off ¹/₃₆₀ of the circumference
a law in trigonometry: the ratio of each side of a plane triangle to the sine of the opposite angle is the same for all three sides and angles
a law in trigonometry: the square of a side of a plane triangle equals the sum of the squares of the remaining sides minus twice the product of those sides and the cosine of the angle between them

